Binary Search Trees (BST) is used for many things that we might not be aware of. For instance: in compilers to generate syntax trees, cryptography and in compressions algorithms used in JPG and MP3. However, search trees need to be balanced to be fast. So, we are going to discuss how to keep the BST balanced as you add and remove elements.
In this post, we are going to explore different techniques to balance a tree. We are going to use rotations to move nodes around and the AVL algorithm to keep track if the tree is balanced or needs adjustments. Let’s dig in!
You can find all these implementations and more in the Github repo: https://github.com/amejiarosario/dsa.js
This post is part of a tutorial series:
Learning Data Structures and Algorithms (DSA) for Beginners
Self-balanced Binary Search Trees 👈 you are here
Let’s start by defining what is a “balanced tree” and the pitfalls of an “unbalanced tree”.
Balanced vs. Unbalanced Binary Search Tree
As discussed in the previous post the worst nightmare for a BST is to be given numbers in order (e.g. 1, 2, 3, 4, 5, 6, 7, …).
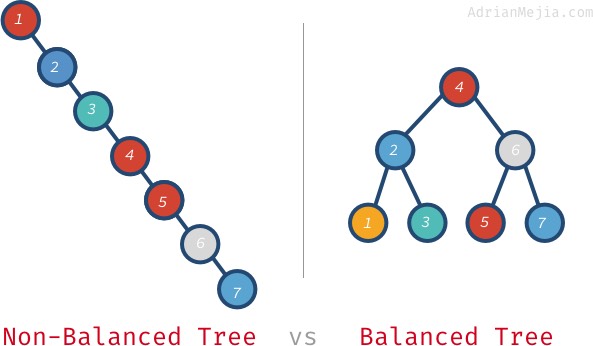
If we ended up with a tree like the one on the left, we are screwed because performance will go to the floor. To find out if a node is on the tree or not, you will have to visit every node when the tree is unbalanced. That takes O(n), while if we keep the node balanced in every insertion or deletion, we could have O(log n).
Again, this might not look like a big difference, but when you have a million nodes, the difference is huge! We are talking about visiting 1,000,000 nodes vs. visiting 20!
“Ok, I’m sold. How do I keep the tree balanced?” I’m glad you asked 😉. Well, let’s first learn when to tell that a tree is unbalanced.
When a tree is balanced/non-balanced?
Take a look at the following trees and tell which one is balanced and which one is not.
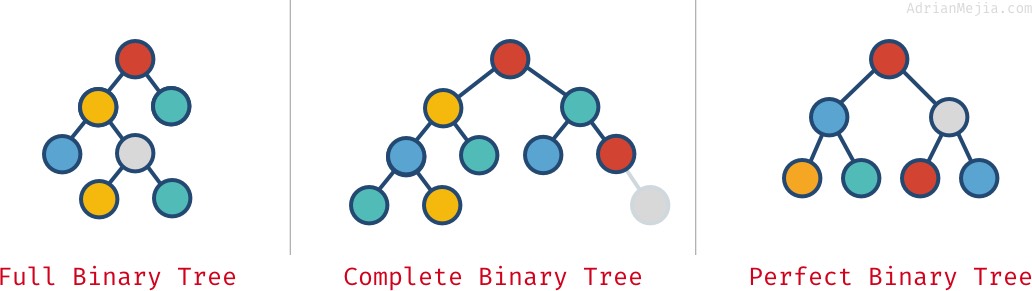
Well, a tree is definately balanced when is a perfect tree (all the levels on the tree have maximum number of nodes). But what about full trees or complete trees ?
The “complete tree” looks somewhat balanced, right? What about the full tree? Well, it starts to get tricky. Let’s work on a definition.
A tree is balanced if:
- The left subtree height and the right subtree height differ by at most 1.
- Visit every node making sure rule #1 is satisfied.
Note: Height of a node is the distance (edge count) from the farthest child to itself.
For instance, if you have a tree with seven nodes:
1 | 10 |
If you check the subtrees’ heights (edge counts to farthest leaf node) recursively you will notice they never differ by more than one.
10descendants:- Left subtree
5has a height of 1, while right subtree20has a height of2. The difference is one so: Balanced!
- Left subtree
20descendants:- Left subtree
15has a height of1, while right subtree30has a height of 0. So the diff is1: Balanced!
- Left subtree
On the other hand, take a look at this tree:
1 | 40 |
Let’s check the height of the subtree recursively:
40descendants:- Left subtree
35has a height of 1, while right subtree60has a height of2. The difference is one so: Balanced!
- Left subtree
60descendants:- Left subtree
50has a height of2, while the right subtree (none) has a height of0. The difference between2and0is more than one, so: NOT balanced!
- Left subtree
Hopefully, now you can calculate balanced and unbalanced trees.
What can we do when we find an unbalanced tree? We do rotations!
If we take the same tree as before and move 50 to the place of 60 we get the following:
1 | 40 |
After rotating 60 to the right, It’s balanced! Let’s learn all about it in the next section.
Tree rotations
Before throwing any line of code, let’s spend some time thinking about how to balance small trees using rotations.
Left Rotation
Let’s say that we have the following tree with ascending values: 1-2-3
1 | 1* 2 |
To perform a left rotation on node 1, we move it down as it’s children’s (2) left descendant.

This is called single left rotation or Left-Left (LL) rotation.
For the coding part, let’s do another example:
1 | 1 1 |
To define the tree, we are using TreeNode that we developed in the previous post.
1 | const n1 = new TreeNode(1); |
In this case, we are rotating 2 to the left. Let’s implement the leftRotation function.
1 | function leftRotation(node) { |
Notice that we are using a utility function to swap parents called swapParentChild.
1 | function swapParentChild(oldChild, newChild, parent) { |
We are using this function to make 1 the parent of 3. We are going to use it rotation right as well.
Right Rotation
We have the following tree with descending values 4-3-2-1:
1 | 4 4 |
To perform a right rotation on node 3, we move it down as its child 2‘s right descendant.

This is called single right rotation or Right-Right (RR) rotation.
The code is pretty similar to what we did on the left rotation:
1 | function rightRotation(node) { |
The rightRotation does the following:
- First, we swap
4‘s child: before it was3and after the swap is2(line 5). - Later, we make
3the right child of 2 (line 8) and - Finally, we clean up the
3right child reference to null (line 9).
Now that know how single rotations work to the left and right we can combine them: left-right and right-left rotations.
Left-Right Rotation
If we insert values on a BST in this order: 3-1-2. We will get an unbalanced tree. To balance the tree, we have to do a leftRightRotation(3).
1 | 3* 2* |
Double rotations are a combination of the other two rotations we discussed in (LL and RR):
If we expand the left-right-rotation into the two single rotations we would have:
1 | 3* 3* |
- left-rotation(1): We do a left rotation on the nodes’ left child. E.g.
1. - right-rotation(3): right rotation on the same node. E.g.
3.

This double rotation is called Left-Right (LR) rotation.
1 | function leftRightRotation(node) { |
The code is straightforward since we leverage the leftRotation and rightRotation that we did before.
Right-Left Rotation
When we insert nodes on the following order: 1-3-2, we need to perform a rightLeftRotation(1) to balance the tree.
1 | 1* 1* |
The code to is very similar to LR rotation:
1 | function rightLeftRotation(node) { |
We know all the rotations needed to balanced any binary tree. Let’s go ahead, use the AVL algorithm to keep it balanced on insertions/deletions.
AVL Tree Overview
AVL Tree was the first self-balanced tree invented. It is named after the two inventors Adelson-Velsky and Landis. In their self-balancing algorithm if one subtree differs from the other by at most one, then rebalancing is done using rotations.
We already know how to do rotations from the previous sections; the next step is to figure out the subtree’s heights. We are going to call balance factor, the diff between the left and right subtree on a given node.
balanceFactor = leftSubtreeHeight - rightSubtreeHeight
If the balance factor is bigger than 1 or less than -1 then, we know we need to balance that node. We can write the balance function as follows:
1 | function balance(node) { |
Based on the balance factor, there four different rotation that we can do: RR, LL, RL, and LR. To know what rotation to do we:
- Take a look into the given
node‘sbalanceFactor. - If the balance factor is
-1,0or1we are done. - If the node needs balancing, then we use the node’s left or right balance factor to tell which kind of rotation it needs.
Notice that we haven’t implemented the node.balanceFactor attribute yet, but we are going to do that next.
One of the easiest ways to implement subtree heights is by using recursion. Let’s go ahead and add height-related properties to TreeNode class:
1 | get height() { |
To understand better what’s going on, let’s do some examples.
Tree with one node
Let’s start with a single root node:
1 | 40* |
- Since this node doesn’t have left nor right children then
leftSubtreeHeightandrightSubtreeHeightwill return0. - Height is
Math.max(this.leftSubtreeHeight, this.rightSubtreeHeight)which isMath.max(0, 0), so height is0. - Balance factor is also zero since
0 - 0 = 0.
Tree with multiple nodes
Let’s try with multiple nodes:
1 | 40 |
balanceFactor(45)
- As we saw leaf nodes doesn’t have left or right subtree, so their heights are 0, thus balance factor is 0.
balanceFactor(50)
leftSubtreeHeight = 1andrightSubtreeHeight = 0.height = Math.max(1, 0), so it’s1.- Balance factor is
1 - 0, so it’s1as well.
balanceFactor(60)
leftSubtreeHeight = 2andrightSubtreeHeight = 0.height = Math.max(2, 0), so it’s2.- Balance factor is
2 - 0, so it’s2and it’s UNBALANCED!
If we use our balance function on node 60 that we developed, then it would do a rightRotation on 60 and the tree will look like:
1 | 40 |
Before the height of the tree (from the root) was 3, now it’s only 2.
Let’s put all together and explain how we can keep a binary search tree balanced on insertion and deletion.
AVL Tree Insertion and Deletion
AVL tree is just a layer on top of a regular Binary Search Tree (BST). The add/remove operations are the same as in the BST, the only difference is that we run the balance function after each change.
Let’s implement the AVL Tree.
1 | const BinarySearchTree = require('./binary-search-tree'); |
If you need to review the dependencies here are the links to the implementations:
The balanceUpstream function gets executed after an insertion or deletion.
1 | function balanceUpstream(node) { |
We go recursively using the balance function on the nodes’ parent until we reach the root node.
In the following animation, we can see AVL tree insertions and deletions in action:
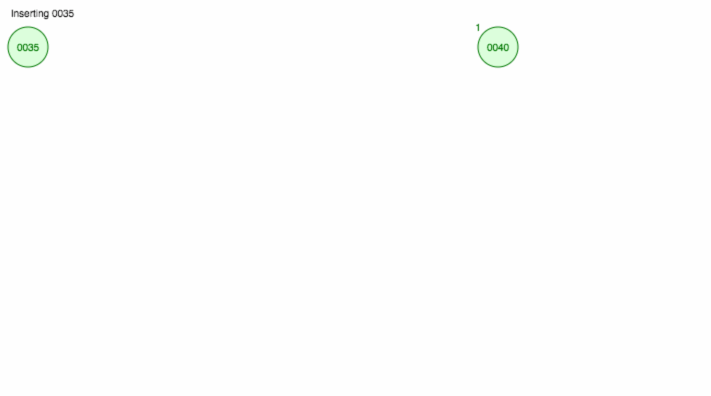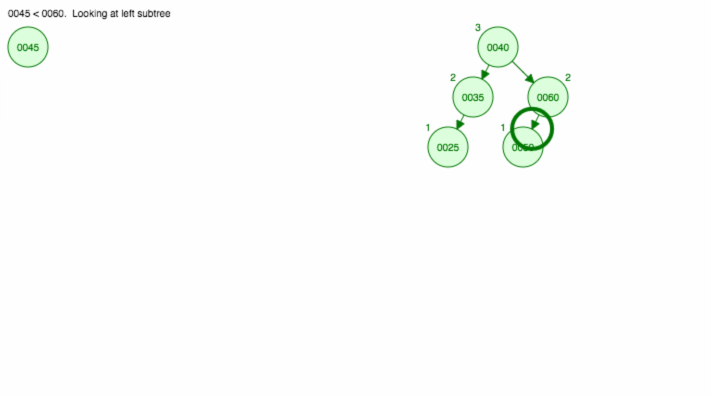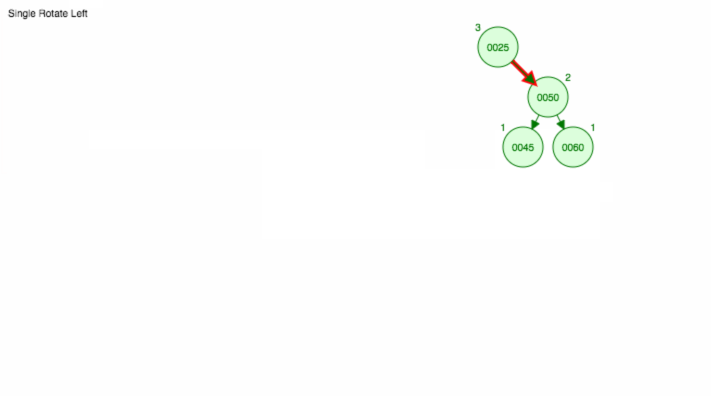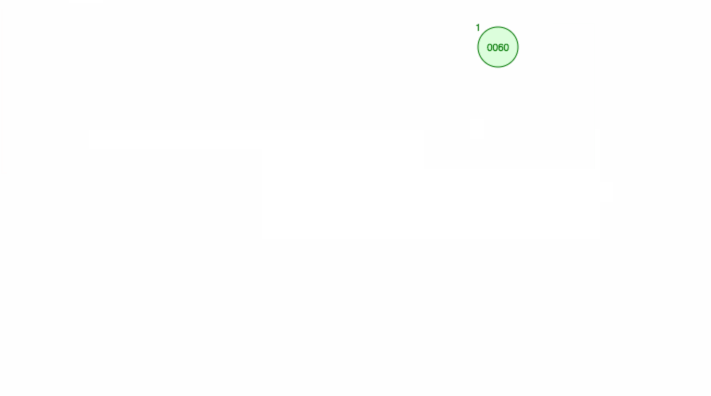
You can also check the test files to see more detailed examples of how to use the AVL trees.
That’s all folks!
Summary
In this post, we explored the AVL tree, which is a particular binary search tree that self-balance itself after insertions and deletions of nodes. The operations of balancing a tree involve rotations, and they can be single or double rotations.
Single rotations:
- Left rotation
- Right rotation
Double rotations:
- Left-Right rotation
- Right-Left rotation
You can find all the code developed here in the
Github.
You can star it to keep it handy.


