Summary
Learn how to compare algorithms and develop code that scales! In this post, we cover 8 Big-O notations and provide an example or 2 for each. We are going to learn the top algorithm’s running time that every developer should be familiar with. Knowing these time complexities will help you to assess if your code will scale. Also, it’s handy to compare multiple solutions for the same problem. By the end of it, you would be able to eyeball different implementations and know which one will perform better without running the code!
In the previous post, we saw how Alan Turing saved millions of lives with an optimized algorithm. In most cases, faster algorithms can save you time, money and enable new technology. So, this is paramount to know how to measure algorithms’ performance.
What is time complexity?
To recap time complexity estimates how an algorithm performs regardless of the kind of machine it runs on. You can get the time complexity by “counting” the number of operations performed by your code. This time complexity is defined as a function of the input size n using Big-O notation. n indicates the input size, while O is the worst-case scenario growth rate function.
We use the Big-O notation to classify algorithms based on their running time or space (memory used) as the input grows. The O function is the growth rate in function of the input size n.
Here are the big O cheatsheet and examples that we will cover in this post before we dive in. Click on them to go to the implementation. 😉
| Big O Notation | Name | Example(s) |
|---|---|---|
| O(1) | Constant | # Odd or Even number, # Look-up table (on average) |
| O(log n) | Logarithmic | # Finding element on sorted array with binary search |
| O(n) | Linear | # Find max element in unsorted array, # Duplicate elements in array with Hash Map |
| O(n log n) | Linearithmic | # Sorting elements in array with merge sort |
| O(n2) | Quadratic | # Duplicate elements in array **(naïve)**, # Sorting array with bubble sort |
| O(n3) | Cubic | # 3 variables equation solver |
| O(2n) | Exponential | # Find all subsets |
| O(n!) | Factorial | # Find all permutations of a given set/string |
Now, Let’s go one by one and provide code examples!
You can find all these implementations and more in the Github repo: https://github.com/amejiarosario/dsa.js
This post is part of a tutorial series:
Learning Data Structures and Algorithms (DSA) for Beginners
Eight time complexities that every programmer should know 👈 you are here
O(1) - Constant time
O(1) describes algorithms that take the same amount of time to compute regardless of the input size.
For instance, if a function takes the same time to process ten elements and 1 million items, then we say that it has a constant growth rate or O(1). Let’s see some cases.
Examples of constant runtime algorithms:
- Find if a number is even or odd.
- Check if an item on an array is null.
- Print the first element from a list.
- Find a value on a map.
For our discussion, we are going to implement the first and last example.
Odd or Even
Find if a number is odd or even.
1 | function isEvenOrOdd(n) { |
Advanced Note: you could also replace n % 2 with the bit AND operator: n & 1. If the first bit (LSB) is 1 then is odd otherwise is even.
It doesn’t matter if n is 10 or 10,001. It will execute line 2 one time.
Do not be fooled by one-liners. They don’t always translate to constant times. You have to be aware of how they are implemented.
If you have a method like Array.sort() or any other array or object method, you have to look into the implementation to determine its running time.
Primitive operations like sum, multiplication, subtraction, division, modulo, bit shift, etc., have a constant runtime. Did you expect that? Let’s go into detail about why they are constant time. If you use the schoolbook long multiplication algorithm, it would take O(n2) to multiply two numbers. However, most programming languages limit numbers to max value (e.g. in JS: Number.MAX_VALUE is 1.7976931348623157e+308). So, you cannot operate numbers that yield a result greater than the MAX_VALUE. So, primitive operations are bound to be completed on a fixed amount of instructions O(1) or throw overflow errors (in JS, Infinity keyword).
This example was easy. Let’s do another one.
Look-up table
Given a string, find its word frequency data.
1 | const dictionary = {the: 22038615, be: 12545825, and: 10741073, of: 10343885, a: 10144200, in: 6996437, to: 6332195 /* ... */}; |
Again, we can be sure that even if the dictionary has 10 or 1 million words, it would still execute line 4 once to find the word. However, if we decided to store the dictionary as an array rather than a hash map, it would be a different story. In the next section, we will explore what’s the running time to find an item in an array.
Only a hash table with a perfect hash function will have a worst-case runtime of O(1). The ideal hash function is not practical, so some collisions and workarounds lead to a worst-case runtime of O(n). Still, on average, the lookup time is O(1).
O(n) - Linear time
Linear running time algorithms are widespread. These algorithms imply that the program visits every element from the input.
Linear time complexity O(n) means that the algorithms take proportionally longer to complete as the input grows.
Examples of linear time algorithms:
- Get the max/min value in an array.
- Find a given element in a collection.
- Print all the values in a list.
Let’s implement the first example.
The largest item on an unsorted array
Let’s say you want to find the maximum value from an unsorted array.
1 | function findMax(n) { |
How many operations will the findMax function do?
Well, it checks every element from n. If the current item is more significant than max it will do an assignment.
Notice that we added a counter to count how many times the inner block is executed.
If you get the time complexity, it would be something like this:
- Line 2-3: 2 operations
- Line 4: a loop of size n
- Line 6-8: 3 operations inside the for-loop.
So, this gets us 3(n) + 2.
Applying the Big O notation that we learn in the
previous post,
we only need the biggest order term, thus O(n).
We can verify this using our counter. If n has 3 elements:
1 | findMax([3, 1, 2]); |
or if n has 9 elements:
1 | findMax([4,5,6,1,9,2,8,3,7]) |
Now imagine that you have an array of one million items. Do you think it will take the same time? Of course not. It will take longer to the size of the input. If we plot n and findMax running time, we will have a linear function graph.
.jpg)
O(n^2) - Quadratic time
A function with a quadratic time complexity has a growth rate of n2. If the input is size 2, it will do four operations. If the input is size 8, it will take 64, and so on.
Here are some examples of quadratic algorithms:
- Check if a collection has duplicated values.
- Sorting items in a collection using bubble sort, insertion sort, or selection sort.
- Find all possible ordered pairs in an array.
Let’s implement the first two.
Has duplicates
You want to find duplicate words in an array. A naïve solution will be the following:
1 | function hasDuplicates(n) { |
Time complexity analysis:
- Line 2-3: 2 operations
- Line 5-6: double-loop of size n, so
n^2. - Line 7-13: has ~3 operations inside the double-loop
We get 3n^2 + 2.
When we have an asymptotic analysis, we drop all constants and leave the most critical term: n^2. So, in the big O notation, it would be O(n^2).
We are using a counter variable to help us verify. The hasDuplicates function has two loops. If we have an input of 4 words, it will execute the inner block 16 times. If we have 9, it will perform counter 81 times and so forth.
1 | hasDuplicates([1,2,3,4]); |
and with n size 9:
1 | hasDuplicates([1,2,3,4,5,6,7,8,9]); |
Let’s see another example.
Bubble sort
We want to sort the elements in an array. One way to do this is using bubble sort as follows:
1 | function sort(n) { |
You might also notice that for a very big n, the time it takes to solve the problem increases a lot. Can you spot the relationship between nested loops and the running time? When a function has a single loop, it usually translates into a running time complexity of O(n). Now, this function has 2 nested loops and quadratic running time: O(n2).
O(n^c) - Polynomial time
Polynomial running is represented as O(nc), when c > 1. As you already saw, two inner loops almost translate to O(n2) since it has to go through the array twice in most cases. Are three nested loops cubic? If each one visit all elements, then yes!
Usually, we want to stay away from polynomial running times (quadratic, cubic, nc, etc.) since they take longer to compute as the input grows fast. However, they are not the worst.
Triple nested loops
Let’s say you want to find the solutions for a multi-variable equation that looks like this:
3x + 9y + 8z = 79
This naïve program will give you all the solutions that satisfy the equation where x, y, and z < n.
1 | function findXYZ(n) { |
This algorithm has a cubic running time: O(n^3).
** Note:** We could do a more efficient solution to solve multi-variable equations, but this works to show an example of a cubic runtime.
O(log n) - Logarithmic time
Logarithmic time complexities usually apply to algorithms that divide problems in half every time. For instance, let’s say that we want to look for a book in a dictionary. As you know, this book has every word sorted alphabetically. If you are looking for a word, then there are at least two ways to do it:
Algorithm A:
- Start on the first page of the book and go word by word until you find what you are looking for.
Algorithm B:
- Open the book in the middle and check the first word on it.
- If the word you are looking for is alphabetically more significant, then look to the right. Otherwise, look in the left half.
- Divide the remainder in half again, and repeat step #2 until you find the word you are looking for.
Which one is faster? The first algorithms go word by word O(n), while the algorithm B split the problem in half on each iteration O(log n). This 2nd algorithm is a binary search.
Binary search
Find the index of an element in a sorted array.
If we implement (Algorithm A) going through all the elements in an array, it will take a running time of O(n). Can we do better? We can try using the fact that the collection is already sorted. Later, we can divide it in half as we look for the element in question.
1 | function indexOf(array, element, offset = 0) { |
Calculating the time complexity of indexOf is not as straightforward as the previous examples. This function is recursive.
There are several ways to analyze recursive algorithms. For simplicity, we are going to use the Master Method.
Master Method for recursive algorithms
Finding the runtime of recursive algorithms is not as easy as counting the operations. This method helps us to determine the runtime of recursive algorithms. We are going to explain this solution using the indexOf function as an illustration.
When analyzing recursive algorithms, we care about these three things:
- The runtime of the work done outside the recursion (line 3-4):
O(1) - How many recursive calls the problem is divided (line 11 or 14):
1recursive call. Notice only one or the other will happen, never both. - How much
nis reduced on each recursive call (line 10 or 13):1/2. Every recursive call cutsnin half.
- The Master Method formula is the following:
T(n) = a T(n/b) + f(n)
where:
T: time complexity function in terms of the input sizen.n: the size of the input. duh? :)a: the number of sub-problems. For our case, we only split the problem into one subproblem. So,a=1.b: the factor by whichnis reduced. For our example, we dividenin half each time. Thus,b=2.f(n): the running time outside the recursion. Since dividing by 2 is constant time, we havef(n) = O(1).
- Once we know the values of
a,bandf(n). We can determine the runtime of the recursion using this formula:
nlogba
This value will help us to find which master method case we are solving.
For binary search, we have:
nlogba = nlog21 = n0 = 1
- Finally, we compare the recursion runtime from step 2) and the runtime
f(n)from step 1). Based on that, we have the following cases:
Case 1: Most of the work done in the recursion.
If nlogba > f(n),
then runtime is:
O(nlogba)
Case 2: The runtime of the work done in the recursion and outside is the same
If nlogba === f(n),
then runtime is:
O(nlogba log(n))
Case 3: Most of the work is done outside the recursion
If nlogba < f(n),
then runtime is:
O(f(n))
Now, let’s combine everything we learned here to get the running time of our binary search function indexOf.
Master Method for Binary Search
The binary search algorithm slit n in half until a solution is found or the array is exhausted. So, using the Master Method:
T(n) = a T(n/b) + f(n)
- Find
a,bandf(n)and replace it in the formula:
a: the number of sub-problems. For our example, we only split the problem into another subproblem. Soa=1.b: the factor by whichnis reduced. For our case, we dividenin half each time. Thus,b=2.f(n): the running time outside the recursion:O(1).
Thus,
T(n) = T(n/2) + O(1)
- Compare the runtime executed inside and outside the recursion:
- Runtime of the work done outside the recursion:
f(n). E.g.O(1). - Runtime of work done inside the recursion given by this formula
nlogba. E.g. O(nlog21) = O(n0) =O(1).
- Finally, getting the runtime. Based on the comparison of the expressions from the previous steps, find the case it matches.
As we saw in the previous step, the work outside and inside the recursion has the same runtime, so we are in case 2.
O(nlogba log(n))
Making the substitution, we get:
O(nlog21 log(n))
O(n0 log(n))
O(log(n)) 👈 this is the running time of a binary search
O(n log n) - Linearithmic
Linearithmic time complexity it’s slightly slower than a linear algorithm. However, it’s still much better than a quadratic algorithm (you will see a graph at the very end of the post).
Examples of Linearithmic algorithms:
- Efficient sorting algorithms like merge sort, quicksort, and others.
Mergesort
What’s the best way to sort an array? Before, we proposed a solution using bubble sort that has a time complexity of O(n2). Can we do better?
We can use an algorithm called mergesort to improve it.
This is how mergesort works:
- We are going to divide the array recursively until the elements are two or less.
- We know how to sort two items, so we sort them iteratively (base case).
- The final step is merging: we merge in taking one by one from each array such that they are in ascending order.
Here’s the code for merge sort:
1 | /** |
As you can see, it has two functions, sort and merge. Merge is an auxiliary function that runs once through the collection a and b, so it’s running time is O(n). Let’s apply the Master Method to find the running time.
Master Method for Mergesort
We are going to apply the Master Method that we explained above to find the runtime:
Let’s find the values of:
T(n) = a T(n/b) + f(n)a: The number of sub-problems is 2 (line 20). So,a = 2.b: Each of the sub-problems dividesnin half. So,b = 2f(n): The work done outside the recursion is the functionmerge, which has a runtime ofO(n)since it visits all the elements on the given arrays.
Substituting the values:
T(n) = 2 T(n/2) + O(n)
- Let’s find the work done in the recursion:
nlogba.
nlog22
n1 = n
- Finally, we can see that recursion runtime from step 2) is O(n) and also the non-recursion runtime is O(n). So, we have the case 2 :
O(nlogba log(n))
O(nlog22 log(n))
O(n1 log(n))
O(n log(n)) 👈 this is running time of the merge sort
O(2^n) - Exponential time
Exponential (base 2) running time means that the calculations performed by an algorithm double every time as the input grows.
Examples of exponential runtime algorithms:
- Power Set: finding all the subsets on a set.
- Fibonacci.
- Travelling salesman problem using dynamic programming.
Power Set
To understand the power set, let’s imagine you are buying a pizza. The store has many toppings that you can choose from, like pepperoni, mushrooms, bacon, and pineapple. Let’s call each topping A, B, C, D. What are your choices? You can select no topping (you are on a diet ;), you can choose one topping, or two or three or all of them, and so on. The power set gives you all the possibilities (BTW, there 16 with four toppings, as you will see later)
Finding all distinct subsets of a given set. For instance, let’s do some examples to try to come up with an algorithm to solve it:
1 | powerset('') // => [''] |
Did you notice any pattern?
- The first returns an empty element.
- The second case returns the empty element + the 1st element.
- The 3rd case returns precisely the results of the 2nd case + the same array with the 2nd element
bappended to it.
What if you want to find the subsets of abc? Well, it would be precisely the subsets of ‘ab’ and again the subsets of ab with c appended at the end of each element.
As you noticed, every time the input gets longer, the output is twice as long as the previous one. Let’s code it up:
1 | function powerset(n = '') { |
If we run that function for a couple of cases we will get:
1 | powerset('') // ... |
As expected, if you plot n and f(n), you will notice that it would be exactly like the function 2^n. This algorithm has a running time of O(2^n).
** Note:** You should avoid functions with exponential running times (if possible) since they don’t scale well. The time it takes to process the output doubles with every additional input size. But exponential running time is not the worst yet; others go even slower. Let’s see one more example in the next section.
O(n!) - Factorial time
Factorial is the multiplication of all positive integer numbers less than itself. For instance:
5! = 5 x 4 x 3 x 2 x 1 = 120
It grows pretty quickly:
20! = 2,432,902,008,176,640,000
As you might guess, you want to stay away, if possible, from algorithms that have this running time!
Examples of O(n!) factorial runtime algorithms:
- Permutations of a string.
- Solving the traveling salesman problem with a brute-force search
Let’s solve the first example.
Permutations
Write a function that computes all the different words that can be formed given a string. E.g.
1 | getPermutations('a') // => [ 'a'] |
How would you solve that?
A straightforward way will be to check if the string has a length of 1. If so, return that string since you can’t arrange it differently.
For strings with a length bigger than 1, we could use recursion to divide the problem into smaller problems until we get to the length 1 case. We can take out the first character and solve the problem for the remainder of the string until we have a length of 1.
1 | function getPermutations(string, prefix = '') { |
If print out the output, it would be something like this:
1 | getPermutations('ab') // ab, ba... |
I tried with a string with a length of 10. It took around 8 seconds!
1 | time node ./lib/permutations.js |
I have a little homework for you:
Can you try with a permutation with 11 characters? ;) Comment below on what happened to your computer!
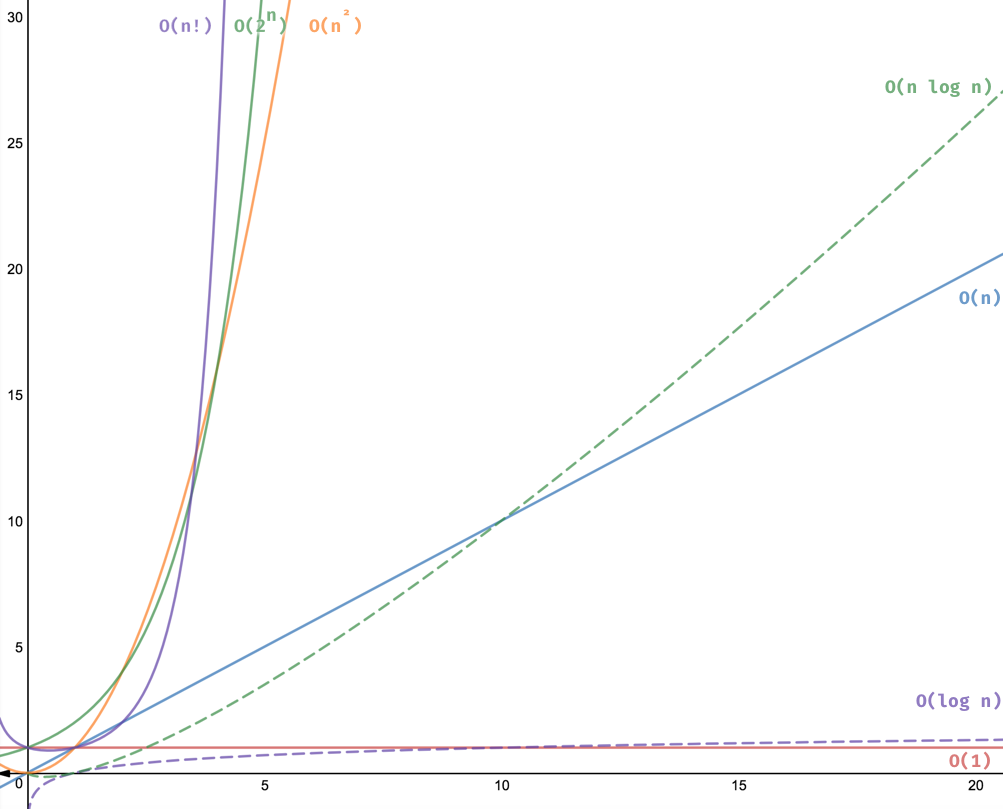
All running complexities graphs
We explored the most common algorithms running times with one or two examples each! They should give you an idea of how to calculate your running times when developing your projects. Below you can find a chart with a graph of all the time complexities that we covered:
Mind your time complexity!


