Graphs are one of my favorite data structures because you can model many real-life situations with them. Such problems involve finding the shortest paths between 2 or more locations, scheduling courses, finding relationships in family trees, solving mazes, and many more! As a result, it’s ubiquitous in tech interview questions. In this article, we are going to demystify it.

In this article you will learn:

  1. 10 steps to avoid getting stuck during coding questions in interviews
  2. How to translate a maze or some “real life” problems into a graph.
  3. How to solve problems using Graph traversing algorithms such as Breadth-First Search (BFS) or Depth-First Search.
  4. When can you use only BFS or DFS or both?

Graph Representations

A Graph can be represented in many ways depending on the problem as a class, Map + Array/Set, implicit graph or adjacency matrix.

TL;DR: When building reusable libraries, you can go with the Graph class implementation. However, when solving a problem quickly (during interviews or one-off problems), go with the implicit implementation if possible or Map+Array representation if you need to build the graph upfront. Don’t use adjacency matrix since it usually uses more memory than other alternatives.

Graph as a Class

You can use OOP to represent graphs, like this:

Graph ClassFull Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
class Graph {
  constructor() { /* ... */ }

  addVertex(value) { /* ... */ }
  removeVertex(value) { /* ... */ }
  addEdge(source, destination) { /* ... */ }
  removeEdge(source, destination) { /* ... */ }

  areAdjacents(source, destination) { /* ... */ }
  areConnected(source, destination) { /* ... */ }
  findPath(source, destination, path = new Map()) { /* ... */ }
  findAllPaths(source, destination, path = new Map()) { /* ... */ }
}

Graph as a class:

  • Very useful for creating libraries or reusable algorithms (find a path, are connected, etc.).
  • OOP Style.
  • Might be time consuming to implement during coding interviews.

Graph as Map + Array

Other way to represent graph is like an Map + Array:

1
2
3
4
5
const graph = {
  a: ['b', 'c'],
  b: ['c'],
  c: [],
};

ES6+ Map:

1
2
3
4
5
const graph = new Map([
  ['a', ['b', 'c']],
  ['b', ['c']],
  ['c', []],
]);

Graph as a HashMap:

  • Very quick to implement
  • Might not be reusable since it’s tailor to the specific problem in hand.
  • Build the entire graph before solving the problem.

Implicit Graph

Some times you don’t have to build a graph upfront. You can calculate adjacent nodes as you go.

For instance, this a template for finding a node in an implicit graph using BFS:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function bfs(target) {
  const queue = [[0, 0]]; // 1. Initialize queue with Node and current distance 0
  const seen = new Set(0); // 2. Initialize set

  for (const [current, distance] of queue) { // 3. Loop until the queue is empty
    if (current === target) return distance; // 4. Check dequeued is solution
    for (const [neighbor, currDist] of getNeighbors(node)) { // 5. Get next possible moves (neighbor nodes)
      if (seen.has(neighbor) continue; // 6. Skip seen nodes
      seen.add(neighbor); // 7. Mark next node as seen.
      queue.push([neighbor, currDist + 1]); // 8. Add neighbor to queue and increase the distance.
    }
  }

  return -1; // 9. If you didn't find the answer, return something like -1/null/undefined.
}

function getNeighbors(node) {
  // TODO: implement based on the problem.
}

Graph on the go:

  • Quick to implement
  • Might not be reusable since it’s tailor to the specific problem in hand.
  • It doesn’t need to build the complete graph up-front; it will discover adjacent nodes as it goes.

Let’s do some examples of each one so we can drive these concepts home!

Solving graph problems

Let’s see how you can use the afore mention implementations to solve real interview questions.

Explicit Graph Structure (Map + Array)

Let’s say you are working for a genealogy company, and you need to find if two people are related given a family tree (graph).

In this case, we can translate the family tree into a graph, where the nodes are the people, and the edges are their relationships (Father/Mother, Son/Daugther, etc.)

Let’s take a family for instance and represent it as a graph:

The Simpson Family Tree Example

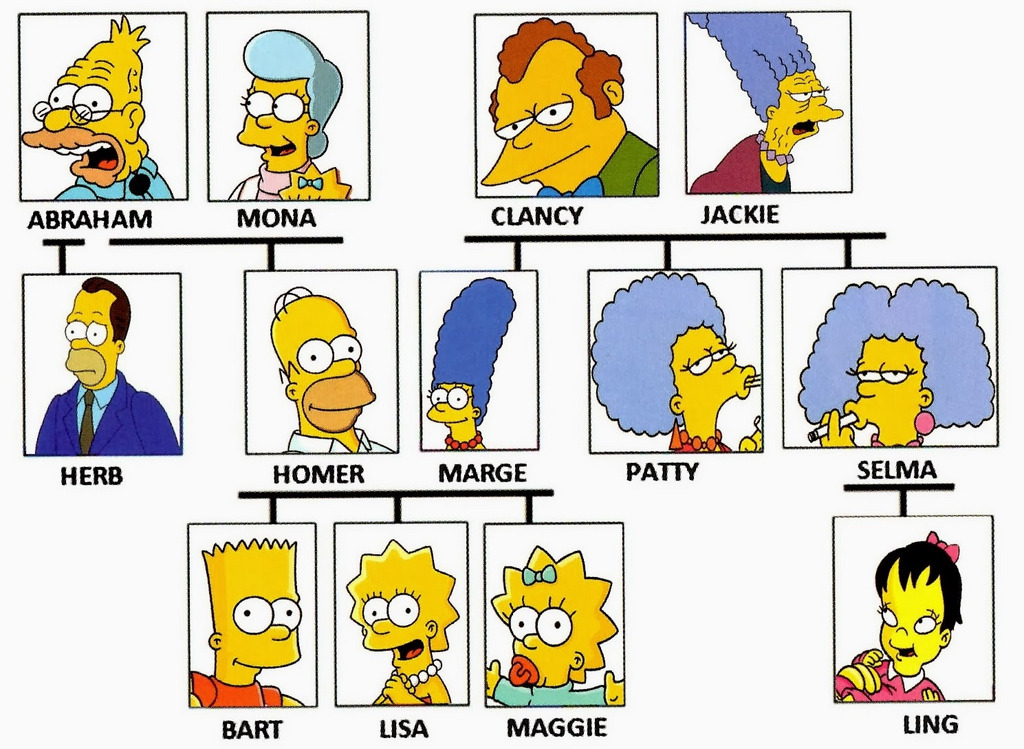
This might be something like this:

1
2
3
4
// people:
nodes = ["Bart", "Homer", "Marge", "Lisa", "Moe", "Herb", "Abraham", "Mona", "Selma", "Clancy", "Jackie", "Bob"];
// relationships:
edges = [["Bart","Homer"],["Bart","Marge"],["Lisa","Homer"],["Lisa","Marge"],["Herb","Abraham"],["Herb","Mona"],["Homer","Abraham"],["Homer","Mona"],["Selma","Clancy"],["Selma","Jackie"],["Marge","Clancy"],["Marge","Jackie"],["Bob","Herb"]];

Interview Question: Given a graph (nodes and edges) and queries return for each query element true if they are related or false if they are not.

Example 1:

  • Input:

    1
    2
    3
    nodes = ["Bart", "Homer", "Moe"]
    edges = [["Bart","Homer"]]
    queries = [["Bart","Homer"], ["Bart","Moe"]];

  • Output:

    1
    [true, false]

    Bart and Homer are related, so the first element is true; Bart and Moe are NOT related, so the 2nd element is false.

  • Function signature:

1
2
3
function findRelated(nodes: any[], edges: [any, any][], queries: [any, any][]): boolean[] {
  // TODO: Implement
}

Here are some ideas on how to solve this problem:

  • We need to traverse the graph from a starting point to a destination.
  • If there’s a path, the two people are related (e.g., Home and Bart)
  • If no path is found, then the two people are NOT related (e.g., Bart and Moe).
  • We can solve this problem by using DFS or BFS.

Do you want to give it a try before looking at the solution? When you are ready, hit run!

function findRelated(nodes, edges, queries) {
  // Write your code here
}

// or here ;)

// ---------------------
// ------- Tests -------
// ---------------------
const assert = require('assert');
let nodes, edges, queries, expected;

// TEST 1
nodes = ["Bart", "Homer", "Marge", "Lisa", "Moe"]; // people
edges = [["Bart","Homer"],["Bart","Marge"],["Lisa","Homer"],["Lisa","Marge"]]; // relationships
queries = [['Bart', 'Lisa'], ['Homer', 'Moe']]; // questions
expected = [true, false];
assert.deepEqual(findRelated(nodes, edges, queries), expected);

// TEST 2
nodes = [1,2,3,4,5];
edges = [[1,2],[1,3],[2,5]];
queries = [[1, 1], [1, 2], [1, 4], [1, 5]];
expected = [true, true, false, true];
assert.deepEqual(findRelated(nodes, edges, queries), expected);

// TEST 3
nodes = ["Bart", "Homer", "Marge", "Lisa", "Moe", "Herb", "Abraham", "Mona", "Selma", "Clancy", "Jackie", "Bob"];
edges = [["Bart","Homer"],["Bart","Marge"],["Lisa","Homer"],["Lisa","Marge"],["Herb","Abraham"],["Herb","Mona"],["Homer","Abraham"],["Homer","Mona"],["Selma","Clancy"],["Selma","Jackie"],["Marge","Clancy"],["Marge","Jackie"],["Bob","Herb"]];
queries = [['Bart', 'Lisa'], ['Homer', 'Moe'], ['Lisa', 'Bob'], ['Bart', 'Selma'], ['Moe', 'Lisa']];
expected = [true, false, true, true, false];
assert.deepEqual(findRelated(nodes, edges, queries), expected);

console.log('All tests passed! 👏 🎂');

Here’s my solution to this problem…

Solution and Explanation for find related

The very first thing that we need to do is to build the graph.

1
2
3
4
5
6
7
8
9
function findRelated(nodes, edges, queries) {
  const graph = nodes.reduce((map, node) => map.set(node, []), new Map());
  edges.forEach(([u, v]) => {
    graph.get(u).push(v);
    graph.get(v).push(u); // undirected graph (2-ways)
  });

  return queries.map(([u, v]) => isRelated(graph, u, v));
}

How does it work?

  • The first function, findRelated builds the graph. We are using an undirected graph, so we have to add the relationship both ways
  • After creating the graph, we iterate over each query and use the helper function isRelated to test if connected.

The isRelated function can be implemented as a BFS or DFS.

Let’s see BFS first:

  • The helper function isRelated, have a start and destination node. We use a Queue to navigate the graph.
  • We also need a Set to keep track of the visited nodes, otherwise, we can fall into an infinite loop.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
function isRelated (graph, start, target) {
    const queue = [start];
    const seen = new Set([start]);

    for (let node of queue) {
        if (node === target) return true;
        graph.get(node).forEach(adj => {
            if (seen.has(adj)) return;
            seen.add(adj);
            queue.push(adj);
        });
    }
    return false;
}

Using DFS:

  • Usually, DFS is implemented using a Stack, we are using a recursive call which makes use the call stack.
  • Notice that we also keep track of the seen nodes using a set.
1
2
3
4
5
6
function isRelated (graph, node, target, seen = new Set()) {
    if (node === target) return true;
    if (seen.has(node)) return false;
    seen.add(node);
    return graph.get(node).some(adj => isRelated(graph, adj, target, seen));
}

As you can see, we can either use a BFS or DFS approach to solve the problem. Not all questions are like that. In the next example, you will see that one of them leads to a more optimal solution than the other.

Implicit Graph: Build and Traverse as you go

Let’s solve this example of a combination lock.

Padlock Problem

You have a combination lock. It has 4 wheels that go from 0 to 9. Your job is to find the minimum amount of wheel turns to get to a target combination. The starting point is always 0000. However, there are several combinations that you have to avoid: deadends. If you get into a dead-end, the wheels will not turn anymore. If the target combination is impossible to reach return -1, otherwise return the minimum number of wheel turns.

Examples 1:

  • Input: deadends = [“8888”], target = “0109”
  • Output: 2
  • Explanation: 0000 -> 0009 -> 0109

Examples 2:

  • Input: deadends = [“8887”,”8889”,”8878”,”8898”,”8788”,”8988”,”7888”,”9888”], target = “8888”
  • Output: -1
  • Explanation: We can’t reach without crossing a deadend.

Do you want to give it a try?

function openLock(deadends, target) {
  // your code goes here!
}

// ---------------------
// ------- Tests -------
// ---------------------
const assert = require('assert');
let deadends, target;

deadends = ['8888'];
target = '0109';
assert.deepEqual(openLock(deadends, target), 2, 'Test #1');

deadends = ['8887','8889','8878','8898','8788','8988','7888']
target = '8888';
assert.deepEqual(openLock(deadends, target), 8, 'Test #2');

console.log('All tests passed! 👏 🥦');
Solution for open the lock

We could solve the problem using DFS or BFS. However, BFS is much more performant… why? We are looking for a minimum amount of turns. As soon as BFS found the target, that is guaranteed to be the minimum. However, that’s not the case for DFS. It goes deep and might found a solution quicker, but it might not be the minimum amount of turns. With DFS, we have to traverse ALL possibilities to see which path to the target is the shortest.

Here’s the BFS solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function openLock(deadends, target) {
  const stop = new Set(deadends);
  const queue = [['0000', 0]];
  const seen = new Set(['0000']);

  for (const [current, turns] of queue) {
    if (stop.has(current)) continue;
    if (current === target) return turns;

    for (const next of getNextTurns(current)) {
      if (seen.has(next)) continue;
      seen.add(next);
      queue.push([next, turns + 1]);
    }
  }

  return -1;
};

function getNextTurns (str) {
  return Array.from(str).reduce((arr, char, i) => arr.concat(
      `${ str.slice(0, i) }${ (Number(char) + 1) % 10 }${ str.slice(i+1) }`,
      `${ str.slice(0, i) }${ (Number(char) + 9) % 10 }${ str.slice(i+1) }`,
    ), []);
}

We will generate around 8 combinations on each step, and these 8 combinations create 7 more each one (we skip seen nodes) and so on.

If you want to see more levels of combination take a look here: combinations graph up to 3 levels

Breadth-First-Search (BFS) vs Depth-First-Search (DFS)

The most common graph traversal algorithms are breadth-first-search (BFS) and depth-first-search (DFS). BFS covers all cases adjacent paths nearby and then expand, while DFS goes deep on one way and only comes back when there’s nowhere else to go.

https://upload.wikimedia.org/wikipedia/commons/5/5d/Breadth-First-Search-Algorithm.gif

https://upload.wikimedia.org/wikipedia/commons/7/7f/Depth-First-Search.gif
Breadth-First-Search (BFS) Depth-First-Search (DFS)

In the pictures above, you can see that BFS goes level by level, while DFS goes as deep as it can in a branch.

In general, you want to use DFS when…

  • The solutions are far away from the starting point.
  • If the graph/tree/maze might be wide but not too deep (e.g., graph is finite).
  • There are too many adjacent nodes to be practical for BFS.
  • Usually used for game simulations where the number of possible moves is massive. DFS make a decision, then explore all paths through this decision. And if this decision leads to a win situation, we stop.
  • Real-world applications of DFS: topological sorting (use for scheduling a sequence of jobs or tasks based on their dependencies), spreadsheets, build systems, data serialization, etc.

You want to use BFS when…

  • The solution is near to the starting point.
  • If the graph/tree/maze is extremely deep but not too wide (e.g., the graph might be infinite).
  • The number of adjacent nodes is limited. (e.g., for our case, each cell has 8 next possible moves)
  • Usually used for finding the shortest path between two nodes.
  • Real-world applications of BFS: anything that can benefit from finding the shortest path, such as GPS Navigation systems (Google Maps), Peer to peer (P2P) applications such as the torrent clients. Other usages are web crawlers, social networks, etc.

Since the board is infinite, DFS won’t work for us. If it chooses a path that doesn’t contain the target location, it will never find an end. So, BFS is the right approach here!

Steps to solve algorithmic questions on interviews

In these section, we are going to practice some real interview questions. First, we are going to introduce 10 steps to avoid you getting in stuck in an interview. Finally, we are going to cover some examples. The only way to get better at it is through Practice, Practice, and more Practice.

Ten steps to avoid getting stuck

  1. 👂 Listen/read carefully and repeat the question out loud (in your own words).
  2. 🗣 Ask clarifying questions to help understand the problem better.
  3. 🎨 Create 2-3 examples and draw diagrams about the problem.
  4. 💪 Find a brute force solution as soon as possible (how would you do it manually). But don’t implement it yet!
  5. 🎯 Determine what’s the best time complexity, theoretically. E.g. O(n) or O(m * n), etc.
  6. 🧠 Brainstorm different approaches (Think out loud). State the runtime (Big O) of each one.
  7. 📝 Let’s CODE: Implement the best approach you have so far (or the brute force, better something than nothing) while following a simple and short example. You can write the code while testing multiple cases at once to save time.
  8. 🏃‍♂️ DRY RUN: Test your implementation on your mind. Imagine you are the compiler, and you have to tell the output of EACH LINE. Make fixes as needed. (For some companies, the code execution is disabled (Facebook), and others use a Google Doc (Google), so it’s vital to learn to test the code in your mind.)
  9. 💻 RUN YOUR CODE if allowed
  10. 🐛 Fix issues as they emerge and repeat previews steps if necessary.

Interview Questions for Practice

Here are some exercises for you to practice the ten steps and the solutions to some. These steps are especially necessary when you are not given the function signature nor examples. Sometimes, you have to figure them out by asking questions.

Let’s do a simulation!

Chess Knight Problem ♞

Given an infinite chessboard, find out how many moves does the knight needs to reach a given square on the board.

Asking Clarifying questions

Once you understand the statement, the first thing you need to do before doing any code is to ask clarifying questions. Try to come up with some questions you would ask before looking at my clarifying questions below.

Examples of clarifying questions...
What do you mean by infinite board?
A regular chess board it's an 8x8 grid but for this questions we have a infinite board (very big limits 1M+ x 1M+). This means the solution better be efficient.
How do we know the initial position of the knight?
Let's say it starts in the coordinates 0,0.
How does the knight moves again? Is like an `L`, right?
Yes, It may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L)
Given enough movements does the knight reach every point in the board?

Yes https://upload.wikimedia.org/wikipedia/commons/c/ca/Knights-Tour-Animation.gif

How's the target location given? As an x, y coordinates?
Yes, coordinates relative to the starting point.

After you ask some clarifying questions, the next step is to come up with some examples. Before you write any code, try to identify edge cases and possible scalability problems. Examples are critical to your success! Let’s draw a board with some possible target positions.

The first case, T1, is in the best-case scenario. It’s just one hop away; the second case is compelling because you have to move away from the starting point and then come back. The other two cases are just far away destinations.

Now that you have some examples, it’s time to brainstorm approaches! No coding yet!

If you are familiar with graphs, you might notice that this can be seen as a graph problem. The starting position can be seen as a node, and then each of the next 8 locations are the adjacent nodes.

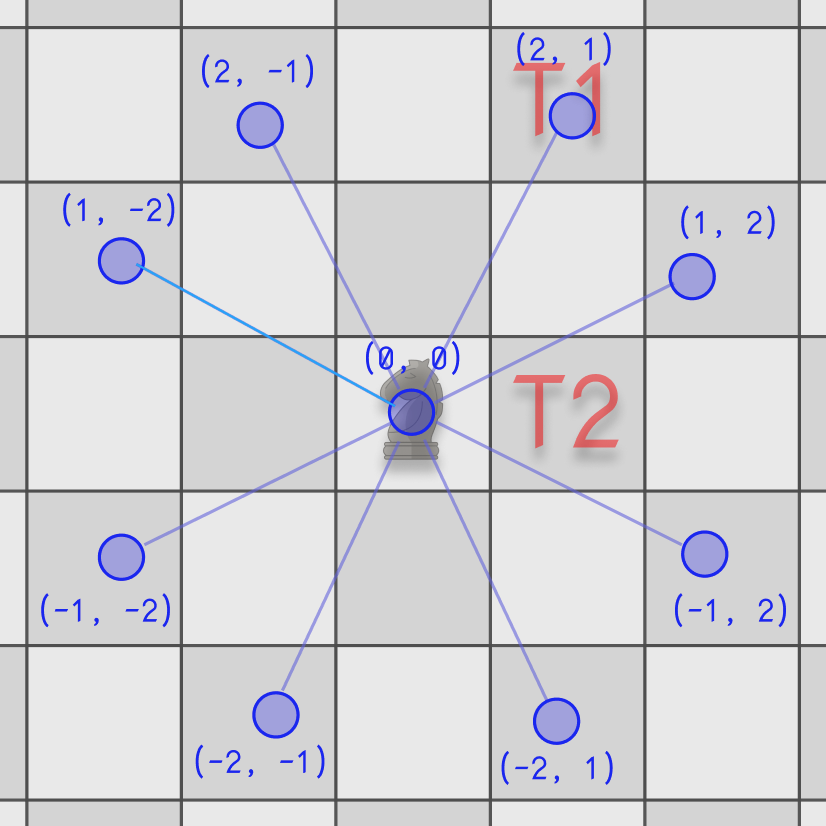
So basically, once we have a starting point and adjacent nodes that we can visit, this can be solved using a graph traversal algorithm.

Solution

First, give it a try yourself before looking at my answer, but don’t spin your wheels for too long. If you haven’t get it working after 35 minutes, take a peek at the answer. Then try again on your own.

/**
 * Given an infinite chessboard, find out how many moves does
 * the knight needs to reach a given square coordinate on the board.
 *
 * @param {Number} dx - Destination x coordinate
 * @param {Number} dy - Destination y coordinate
 * @returns {Number} minimum number of moves to reach target
 */
function knightMoves(dx, dy) {
    // write your awesome code here!
}

// ---------------------
// ------- Tests -------
// ---------------------
const assert = require('assert');

assert.equal(knightMoves(0, 0), 0, 'finds t0');
assert.equal(knightMoves(1, 2), 1, 'finds t1');
assert.equal(knightMoves(0, 1), 3, 'finds t2');
assert.equal(knightMoves(6, -6), 4, 'finds t3');
assert.equal(knightMoves(0, 7), 5, 'finds t4');
assert.equal(knightMoves(170, 123), 99, 'finds far far away galaxies');

console.log('Congrats! 👏👏👏  All tests passed! 🎂');
My answer (click to expand)

Here’s an interview friendly solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function knightMoves(dx, dy) { // destination x and y
  const queue = [[[0, 0], 0]];
  const seen = new Set([0, 0].toString());

  for (const [[x, y], moves] of queue) { // current x and y
    if (x === dx && y === dy) return moves;
    const next = [1, -1].map((i) => [2, -2].map((j) => [[x + i, y + j], [x + j, y + i]])).flat(2);
    for (const [nx, ny] of next) { // next x and y
      if (seen.has([nx, ny].toString())) continue;
      seen.add([nx, ny].toString());
      queue.push([[nx, ny], moves + 1]);
    }
  }

  return -1;
}

What??? No fancy Graph nor Queue class? And less than 20 lines of code?! Yep 😉

We have an old-school array as a Queue, where we store 3 values: the [x, y] coordinate and the number of moves so far. We initialized everything to 0.

It’s vital to keep track of the positions that you have “seen.” Otherwise, you will repeat visited places and make your program very slow or run out of memory! For that, we have a Set.

GOTCHA: the Set in JavaScript for Array values works by reference and not by value. To overcome this issue, we have to convert the array to a string.

1
2
3
4
5
6
7
const s = new Set();

s.add([0, 0]);
console.log(s.has([0, 0])); // false 🙀

s.add([0, 0].toString());
console.log(s.has([0, 0].toString())); // true 👍

Ok, moving on, We reach the for...of loop. Here we dequeue values. Notice that we are NOT using queue.shift(), to take values from the front of the queue. This is because shift has a time complexity of O(n). It will take the first element from the array and then “shift” all the other elements one position. Imagine that you have an array of millions of items. It will move all of them! There are two ways to avoid that overhead; we iterate the queue or implement a queue using a LinkedList.

After we dequeue an element, the first thing we do is to check if it is a solution. If it is, we return the number of movements that took us to get there, and we are done!

If the dequeued element didn’t match the target, we need to calculate the next eight possible positions given the current x and y. Remember a knight moves in L, so it will be translated to 1 position on x and 2 on y or vice-versa:

1
2
const next = [[x + 1, y + 2], [x + 2, y + 1], [x + 2, y - 1], [x + 1, y - 2], [x - 1, y - 2], [x - 2, y - 1], [x - 2, y + 1], [x - 1, y + 2]];
// for x=0, y=0: [[1,2],[2,1],[2,-1],[1,-2],[-1,-2],[-2,-1],[-2,1],[-1,2]]

You can also get fancy and calculate it using two Array.maps

1
2
const next = [1, -1].map((i) => [2, -2].map((j) => [[x + i, y + j], [x + j, y + i]])).flat(2);
// for x=0, y=0: [[1,2],[2,1],[2,-1],[1,-2],[-1,-2],[-2,-1],[-2,1],[-1,2]]

Or also, using two Array.reduces

1
2
const next = [1, -1].reduce((a, i) => [2, -2].reduce((b, j) => [...b, [x + i, y + j], [x + j, y + i]], a), []);
// for x=0, y=0: [[1,2],[2,1],[2,-1],[1,-2],[-1,-2],[-2,-1],[-2,1],[-1,2]]

Once you generate the 8 next positions, you need to add them all to the queue and add +1 to the current place. Finally, we don’t add a location to the queue if we have already seen it before.

That’s it!

How did you do? Paste your solution and questions in the comments section!

Most BFS problems follow the same pattern:

  1. Initialize queue
  2. Initialize set to keep track of the visited positions.
  3. Loop until the queue is empty or you find a solution.
  4. Dequeue element from the queue and check if it’s a solution.
  5. If it’s not part of the solution, move to get the next possible moves (neighbor nodes).
  6. Skip seen nodes.
  7. Mark the next node, as seen.
  8. Add neighbors to queue and increase the distance.
  9. If you didn’t find the answer, return something like -1/null/undefined.

BFS Template

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function bfs(target) {
  const queue = [[0, 0]]; // 1. Initialize queue with Node and current distance 0
  const seen = new Set(0); // 2. Initialize set

  for (const [current, distance] of queue) { // 3. Loop until the queue is empty
    if (current === target) return distance; // 4. Check dequeued is solution
    for (const [neighbor, currDist] of getNeighbors(node)) { // 5. Get next possible moves (neighbor nodes)
      if (seen.has(neighbor) continue; // 6. Skip seen nodes
      seen.add(neighbor); // 7. Mark next node as seen.
      queue.push([neighbor, currDist + 1]); // 8. Add neighbor to queue and increase the distance.
    }
  }

  return -1; // 9. If you didn't find the answer, return something like -1/null/undefined.
}

function getNeighbors(node) {
  // TODO: implement based on the problem.
}

Here’s another exercise to practice

Maze Path

You have a ball at a starting point, that can roll up, down, left and right. However, the ball won’t stop rolling until it hits a wall. Your task is to check if there’s a path from start to destination. You may assume that the borders of the maze are all walls.

The maze is represented in a grid (2d array):

  • Walls are represented as 1.
  • Empty spaces are 0.

E.g.:

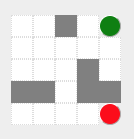maze ball game 
start = [ 0, 4 ]
end = [ 4, 4 ]
maze = [
  [ 0, 0, 1, 0, 0 ],
  [ 0, 0, 0, 0, 0 ],
  [ 0, 0, 0, 1, 0 ],
  [ 1, 1, 0, 1, 1 ],
  [ 0, 0, 0, 0, 0 ]
]

Give it a try!

/**
 * You have a ball at a starting point that can roll up, down, left and right.
 * However, the ball won't stop rolling until it hits a wall.
 * Your tasks is to check if there's a path from start to destination
 * You may assume that the borders of the maze are all walls.
 *
 * @param {number[][]} maze - 2D array where 1 = wall and 0 = empty.
 * @param {number[]} start - [row, col] of the starting point
 * @param {number[]} destination - [row, col] target destination
 * @return {boolean}
 */
function hasPath(maze, start, destination) {

};

// --- testing ---

const assert = require('assert');

assert.equal(hasPath([
  [ 0 ]
], [0, 0], [0, 0]), true, 'should pass case #1');

assert.equal(hasPath([
  [ 1 ]
], [0, 0], [0, 0]), false, 'should pass case #2');

assert.equal(hasPath([
  [ 0, 0, 0 ]
], [0, 0], [0, 2]), true, 'should pass case #3');

assert.equal(hasPath([
    [ 0, 0, 0 ],
], [0, 0], [0, 1]), false, 'should pass case #4');

assert.equal(hasPath([
  [ 0, 1, 0 ],
], [0, 0], [0, 2]), false, 'should pass case #5');

assert.equal(hasPath([
  [ 0, 1, 0 ],
  [ 0, 0, 0 ],
], [0, 2], [0, 0]), true, 'should pass case #6');

assert.equal(hasPath([
  [ 0, 0, 1, 0, 0 ],
  [ 0, 0, 0, 0, 0 ],
  [ 0, 0, 0, 1, 0 ],
  [ 1, 1, 0, 1, 1 ],
  [ 0, 0, 0, 0, 0 ]
], [ 0, 4 ], [ 3, 2 ]), false, 'should pass case #7');

assert.equal(hasPath([
  [ 0, 0, 1, 0, 0 ],
  [ 0, 0, 0, 0, 0 ],
  [ 0, 0, 0, 1, 0 ],
  [ 1, 1, 0, 1, 1 ],
  [ 0, 0, 0, 0, 0 ]
], [ 0, 4 ], [ 4, 4 ]), true, 'should pass case #8');

console.log('Congrats! 👏👏👏  All tests passed! 🍎');
My answer to the maze problem

We can solve this problem using the BFS template. The tricky part is to know that the ball is going to roll until it hit a wall. So, we have to roll in one direction until we hit a wall (1) or end.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
function hasPath(maze, start, dest) {
  const queue = [[start, 0]];
  const seen = new Set([start.join()]);
  const directions = [[0,1], [0,-1], [1,0], [-1,0]]; // right, left, down and up.

  for (let [[r, c], dist] of queue) {
    if (r === dest[0] && c === dest[1] && maze[r] && maze[r][c] === 0) return true;

    for (let [dr, dc] of directions) {
      let nr = r, nc = c; // IMPORTANT: reset coordinates
      while (maze[nr + dr] && maze[nr + dr][nc + dc] === 0) {
          nr += dr;
          nc += dc;
      }
      if (seen.has([nr, nc].join())) continue;
      seen.add([nr, nc].join());
      queue.push([[nr, nc], dist + 1]);
    }
  }

  return false;
};

How did you do? Feel free to ask me any questions below!