Priority Queue Data Structure and Heaps Implemented in JavaScript

A priority queue is a versatile data structure that is good to have under your algorithmic toolbelt. In this post, we discuss, what it is, real-world applications, and we explore two different implementations, the latter one being more robust.

What’s a Priority Queue (PQ)?

A priority queue is a data structure that extends the queue by a priority dimension. Let’s expand both terms. The queue is a list of elements taken in the same order as they arrived. For instance, a line of people waiting to pay at the Supermarket behaves like a queue: first-in, first-served, or FIFO (first in, first out).

The priority queue adds a priority to each element’s value. If we go back to the example of a line of people in a supermarket. You can add preferred lanes, for example, Seniors (65+ years old) and pregnant women. If you have Seniors in the line, you will take them first, even if other people arrived before them. That’s what a priority queue (PQ) does. If all elements in a PQ have the same priority, then it will behave like a regular queue.

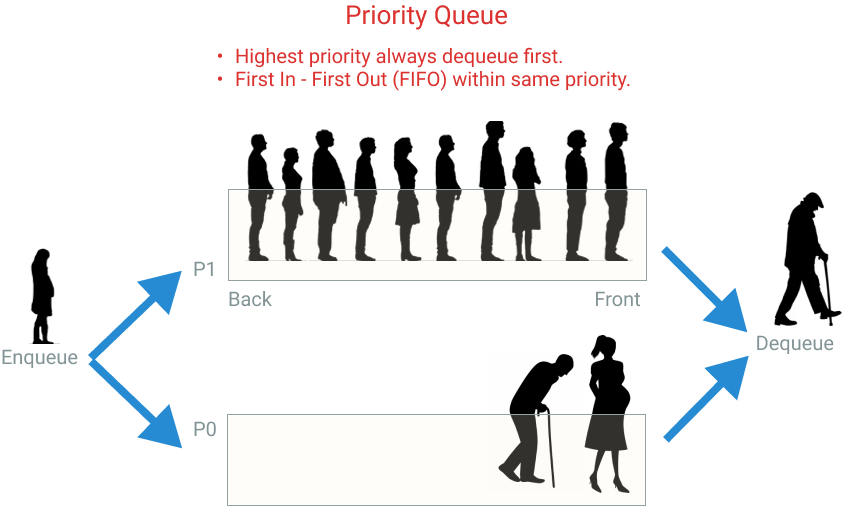
priority queue as line of people

Why a priority queue? Can’t we just have different queues for each priority? That only works if you have a few priorities, but sometimes you have infinite possibilities (e.g., the distance between two points, ETA, etc.). Later in this post, we will explore how we can implement an efficient solution for these cases.

What is a priority queue good for? / Applications

There are many real-world applications for priority queues, such as:

System to triage hospital patients and attend them by their severity order.
Forward network packages in order of urgency (e.g., “real-time video call” should go before “time sync checks,” so to speak)
Scheduling tasks in a system: “critical” goes before “shadow drawing” for instance.
Asynchronous control flows like firing events (or notifying observers) in a certain order.
Keeping track of top k elements efficiently
Keeping track of median numbers in constant time
Used in some graph algorithms like Dijkstra for finding the shortest path between two points. The distance among points is used as a priority.

Some priority queue JavaScript implementations on the wild:

closure-library: heap.js, priorityqueue.js
dsa.js: heap.js, priority-queue.js, min-heap.js, max-heap.js
async : priorityQueue.js, Heap.js.
datastructures-js: heap.js, priorityQueue.js

This tutorial will start with a simple implementation and then build it to a robust implementation while making it easy to follow.

Implementing a Priority Queue (PQ) in JavaScript

JavaScript standard doesn’t provide a default implementation that we can use. So, we are going to define our own. But, even if you use another language that has it in their standard API, it’s still good to know how it works so you can reason about the time complexity of their operations.

Without any further ado, let’s get to it!

Priority Queue operations

As always, there are many ways to solve the same problem. We are going to brainstorm some approaches along with their pros and cons. Yes, there’s never a perfect approach. However, we can learn to analyze the trade-offs and how we can improve our algorithms better.

The essential operations of the priority queue are:

enqueue: insert elements on the queue
dequeue: remove elements from the queue in the same order they were inserted.

Priority queue usually has a comparison function. Since our data could be simple (just an array of numbers where the value and priority are the same) or compound, where we have multiple fields (e.g. the priority could be the age of a student object). The comparator function tells our PQ what we can use as a priority. Here’s an example:

const pq= new PriorityQueue((x, y) => y.age - x.age);
pq.enqueue({ name: 'Maria', age: 23 });
pq.enqueue({ name: 'Nushi', age: 42 });
pq.enqueue({ name: 'Jose', age: 32 });

pq.dequeue(); // { name: 'Nushi', age: 42 }
pq.dequeue(); // { name: 'Jose', age: 32 }
pq.dequeue(); // { name: 'Maria', age: 23 }

As you can see, the comparator function dequeue elements with the highest age first. This is called a Max-PQ. We can invert the minuend and subtrahend to get a Min-PQ. Another possibility to use the name as a priority.

Now that we have a general idea of how a PQ API works let’s explore how we can implement it.

Naive: Priority Queue implemented using Array + Sorting

You can implement a regular queue using an array or linked list. However, priority queues have a new dimension: It needs to sort elements by priority. So, can we just sort a regular array queue every time we insert a new element? Yes, we can! But let’s see how it will perform.

Enqueue

Every time we insert a new element, we need to sort the elements. That’s O(n log n).

Complexity

Time: O(n log n), insertion into an array is constant but sorting takes n log n.
Space: O(n), the space used in memory will grow proportionally to the number of elements in the queue.

Here’s the implementation of the Enqueue method:

class NaivePQ {
  constructor(comparator = (a, b) => a - b) {
    this.array = [];
    this.comparator = comparator;
  }

  /**
   * Insert element
   * @runtime O(n log n)
   * @param {any} value
   */
  add(value) {
    this.array.push(value);
    this.array.sort(this.comparator);
  }

 //...
}

Dequeue

Dequeue removes elements from the PQ. We need to find the element with the highest priority and then return that. The highest number will be first element, so that’s O(1) operation. However, we need to move the rest of the elements to fill the gap. That’s O(n).

Complexity

Time: O(n), finding the top element.
Space: O(n), space is technically O(n-1). However, we just care about the “higher order” term, so O(n).

/**
 * Retrieves and removes the head or returns null if this Heap is empty.
 * @runtime O(n)
 */
remove() {
  if (!this.size) return null;
  const value = this.array.shift(); // remove element
  return value;
}

Improving PQ implementation

Can we do better? We could do nothing after insertion O(1) and then delegate the finding of the element with the highest priority to dequeue (if max-heap). That would be O(n).

O(n) as time complexity is not bad. It’s better than sorting all elements on every insertion O(n log n). Still, how can we improve this? If we use a data structure that keeps the max element at the top in less than O(n), that would be great! Good news, that’s what a heap is for!

Priority Queue implemented using a Heap

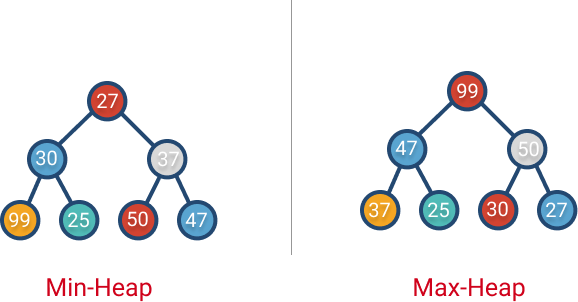
A heap is a tree data structure that keeps to max or min element at the root. So you can have a max-heap or min-heap. Regardless, they have two basic operations: insert and remove.

Conceptually the heaps can be represented as a complete binary tree. With the following rules or invariants:

The parent node should be smaller (or equal) than the two children for a Min-Heap. For a max-heap is the opposite, the parent node should be bigger (or equal) than the two children.
The binary tree should be complete (all levels are completely filled. The only exception is the last level which might not be full, but the ones filled comes from left to right without gaps)

Min-Heap vs Max-Heap

Even though a heap is conceptually a binary tree, it can be implemented using an array since it’s a complete tree. The first element on the array is the root. The following two elements are the root’s children, the 4th and 5th elements are the 2nd element’s children, and so on.

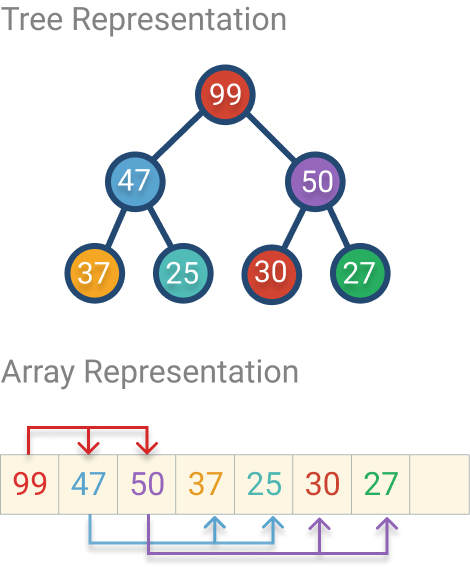
Tree/Heap to Array Representation

You can calculate the following formula to translate tree to array:

parent(i) = Math.ceil(i / 2 - 1)
leftChild(i) = 2 * i + 1
rightChild2(i) = 2 * i + 2

What’s the time complexity of heaps and Priority Queue?

Again the PQ has two primary operations: enqueue and dequeue. So, let’s see how we can do this with a heap.

Enqueue

The algorithm to insert an element in a heap is as follows:

Insert the element into the next empty position (tail).
From that position, “bubble up” the element to keep the min-heap invariant “parent should be smaller than any children” (the opposite if max-heap). If the invariant is broken, fix it by swapping the node with its parent and repeat the process all the way to the root node if necessary.

Here’s an implementation of the Heap. Also we are using a comparator function so we can define the priority.

class Heap {
  constructor(comparator = (a, b) => a - b) {
    this.array = [];
    this.comparator = (i1, i2) => comparator(this.array[i1], this.array[i2]);
  }

  /**
   * Insert element
   * @runtime O(log n)
   * @param {any} value
   */
  add(value) {
    this.array.push(value);
    this.bubbleUp();
  }

  /**
   * Move new element upwards on the Heap, if it's out of order
   * @runtime O(log n)
   */
  bubbleUp() {
    let index = this.size - 1;
    const parent = (i) => Math.ceil(i / 2 - 1);
    while (parent(index) >= 0 && this.comparator(parent(index), index) > 0) {
      this.swap(parent(index), index);
      index = parent(index);
    }
  }
}

This algorithm can keep a heap sorted in O(log n) because it only visits half of the tree at most.

“Why log n?“**,** you asked.

Because that’s the maximum number of swaps that you would have to bubble up the newly inserted element.

I see, but where did you get that log n from?

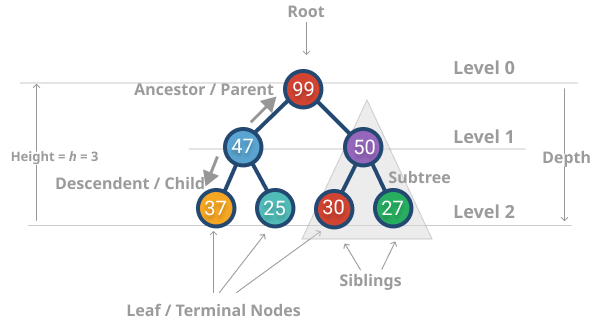
binary tree parts

Well, in a complete binary tree, you double the number of nodes at each level. If you use some intuition and math you can find the following relationship:

Level 0: 2⁰ = 1 node (root)
Level 1: 2¹ = 2 nodes
Level 2: 2² = 4 nodes
Level 3: 2³ = 8 nodes
…
Level h: 2^h = 2^h nodes

Total number of nodes, n: 1 + 2 + 4 + 8 + … + 2^h

So, we have a formula that relates the total number of nodes with the tree’s height. The height is essential because that will be the maximum number of times we would swap nodes when we insert a new element in the Heap.

Using geometric progression and the total number of nodes formulas we have:

` 2^{0}+2^{1}+2^{2}+2^{3}+\cdots +2^{k-1} = \sum _{i=0}^{k-1}2^{i} = 2^{k}-1 `

` n = 2^{h + 1} - 1 `

` \log _{2}(n + 1) = h + 1 `

` h = \log _{2}(n + 1) - 1 `

Well, there you have it. That’s where the log n comes from.

Complexity:

Time: O(log n), in the worst case, you will have to bubble up the inserted element up to the root of the tree. These will involve log n swaps, where n is the total number of nodes.
Space: O(n)

Dequeue

The algorithms for dequeuing an element from a PQ is the following:

Remove the root element
Since the root element is gone, you need to fill the hole by promoting a child to take its place. This process is called “heapify” or bubbleDown. You choose the child that has the min value for min-heap (or max value for max-heap). You do this recursively until you found a leaf (node without children).

Complexity:

Time: O(log n), The maximum number of swaps is given by the tree’s height, which is log n.
Space: O(n).

/**
 * Retrieves and removes the head of this Heap or returns null if this Heap is empty.
 * @runtime O(log n)
 */
remove(index = 0) {
  if (!this.size) return null;
  this.swap(index, this.size - 1); // swap with last
  const value = this.array.pop(); // remove element
  this.bubbleDown(index);
  return value;
}

/**
 * After removal, moves element downwards on the Heap, if it's out of order
 * @runtime O(log n)
 */
bubbleDown(index = 0) {
  let curr = index;
  const left = (i) => 2 * i + 1;
  const right = (i) => 2 * i + 2;
  const getTopChild = (i) => (right(i) < this.size
    && this.comparator(left(i), right(i)) > 0 ? right(i) : left(i));

  while (left(curr) < this.size && this.comparator(curr, getTopChild(curr)) > 0) {
    const next = getTopChild(curr);
    this.swap(curr, next);
    curr = next;
  }
}

You can find the full implementation at: https://github.com/amejiarosario/dsa.js-data-structures-algorithms-javascript/blob/master/src/data-structures/heaps/heap.js

Summary

In these post we learned about the usages of a priority queue and how to implement it with an array+sorting and using array-based heap. We also explored it’s time complexity for each implementation so we can verify that the heap implementation is more efficient.