When we are developing software, we have to store data in memory. However, many types of data structures, such as arrays, maps, sets, lists, trees, graphs, etc., and choosing the right one for the task can be tricky. This series of posts will help you know the trade-offs so that you can use the right tool for the job!

This section will focus on linear data structures: Arrays, Lists, Sets, Stacks, and Queues.

You can find all these implementations and more in the Github repo: https://github.com/amejiarosario/dsa.js

This post is part of a tutorial series:

Learning Data Structures and Algorithms (DSA) for Beginners

  1. Intro to algorithm’s time complexity and Big O notation

  2. Eight time complexities that every programmer should know

  3. Data Structures for Beginners: Arrays, HashMaps, and Lists 👈 you are here

  4. Graph Data Structures for Beginners

  5. Trees Data Structures for Beginners

  6. Self-balanced Binary Search Trees

  7. Appendix I: Analysis of Recursive Algorithms

Data Structures Big-O Cheatsheet

The following table is a summary of everything that we are going to cover.

Bookmark it, pin it, or share it, so you have it at hand when you need it.

Click on the name to go to the section or click on the runtime to go to the implementation

* = Amortized runtime

Name Insert Access Search Delete Comments
Array O(n) O(1) O(n) O(n) Insertion to the end is O(1). Details here.
HashMap O(1) O(1) O(1) O(1) Rehashing might affect insertion time. Details here.
Map (using Binary Search Tree) O(log(n)) - O(log(n)) O(log(n)) Implemented using Binary Search Tree
Set (using HashMap) O(1) - O(1) O(1) Set using a HashMap implementation. Details here.
Set (using list) O(n) - O(n) O(n) Implemented using Binary Search Tree
Set (using Binary Search Tree) O(log(n)) - O(log(n)) O(log(n)) Implemented using Binary Search Tree
Linked List (singly) O(n) - O(n) O(n) Adding/Removing to the start of the list is O(1). Details here.
Linked List (doubly) O(n) - O(n) O(n) Adding/Deleting from the beginning/end is O(1). But, deleting/adding from the middle is O(n). Details here
Stack (array implementation) O(1) - - O(1) Insert/delete is last-in, first-out (LIFO)
Queue (naïve array impl.) O(1) - - O(n) Remove (Array.shift) is O(n)
Queue (array implementation) O(1) - - O(1) Worst time insert is O(n). However amortized is O(1)
Queue (list implementation) O(1) - - O(1) Using Doubly Linked List with reference to the last element.

Note: Binary search trees and trees, in general, will be cover in the next post. Also, graph data structures.

Primitive Data Types

Primitive data types are the most basic elements, where all the other data structures are built upon. Some primitives are:

  • Integers. E.g., 1, 2, 3, …
  • Characters. E.g., a, b, "1", "*"
  • Booleans. E.g., true or false.
  • Float (floating points) or doubles. E.g., 3.14159, 1483e-2.
  • Null values. E.g. null

JavaScript specific primitives:

  • undefined
  • Symbol
  • Number

Note: Objects are not primitive since they are composed of zero or more primitives and other objects.

Array

Arrays are collections of zero or more elements. Arrays are one of the most used data structures because of their simplicity and fast way of retrieving information.

You can think of an array as a drawer where you can store things in the bins.

Array is like a drawer that stores things on bins

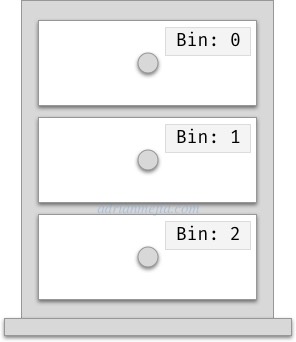
When you want to search for something, you can go directly to the bin number. That’s a constant time operation (O(1)). However, if you forgot what cabinet had, you will have to open one by one (O(n)) to verify its content until you find what you are looking for. That same happens with an array.

Depending on the programming language, arrays have some differences. For some dynamic languages like JavaScript and Ruby, an array can contain different data types: numbers, strings, words, objects, and even functions. In typed languages like Java/C/C++, you have to predefine the Array size and the data type. In JavaScript, it would automatically increase the size of the Array when needed.

Arrays built-in operations

Depending on the programming language, the implementation would be slightly different.

For instance, in JavaScript, we can accomplish append to end with push and append to the beginning with unshift. But also, we have pop and shift to remove from an array. Let’s describe some everyday operations that we are going to use through this post.

Common JS Array built-in functions

Function Runtime Description
array.push O(1) Insert element to the end of the array
array.pop O(1) Remove element to the end of the array
array.shift O(n) Remove element to the beginning of the array
array.unshift O(n) Insert element(s) to the beginning of the array
array.slice O(n) Returns a copy of the array from beginning to end.
array.splice O(n) Changes (add/remove) the array

Insert element on an array

There are multiple ways to insert elements into an array. You can append new data to the end or add it to the beginning of the collection.

Let’s start with append to tail:

1
2
3
4
5
6
7
function insertToTail(array, element) {
  array.push(element);
  return array;
}

const array = [1, 2, 3];
console.log(insertToTail(array, 4)); // => [ 1, 2, 3, 4 ]

Based on the language specification, push just set the new value at the end of the Array. Thus,

The Array.push runtime is a O(1)

Let’s now try appending to head:

1
2
3
4
5
6
7
function insertToHead(array, element) {
  array.unshift(element);
  return array;
}

const array = [1, 2, 3];
console.log(insertToHead(array, 0)); // => [ 0, 1, 2, 3 ]

What do you think is the runtime of the insertToHead function? It looks the same as the previous one, except that we are using unshift instead of push. But there’s a catch! unshift algorithm makes room for the new element by moving all existing ones to the next position in the Array. So, it will iterate through all the elements.

The Array.unshift runtime is an O(n)

Access an element in an array

If you know the index for the element that you are looking for, then you can access the element directly like this:

1
2
3
4
5
6
7
function access(array, index) {
  return array[index];
}

const array = [1, 'word', 3.14, {a: 1}];
access(array, 0); // => 1
access(array, 3); // => {a: 1}

As you can see in the code above, accessing an element on an array has a constant time:

Array access runtime is O(1)

Note: You can also change any value at a given index in constant time.

Search an element in an array

Suppose you don’t know the index of the data that you want from an array. You have to iterate through each element on the Array until we find what we are looking for.

1
2
3
4
5
6
7
8
9
10
11
function search(array, element) {
  for (let index = 0; index < array.length; index++) {
    if(element === array[index]) {
      return index;
    }
  }
}

const array = [1, 'word', 3.14, {a: 1}];
console.log(search(array, 'word')); // => 1
console.log(search(array, 3.14)); // => 2

Given the for-loop, we have:

Array search runtime is O(n)

Deleting elements from an array

What do you think is the running time of deleting an element from an array?

Well, let’s think about the different cases:

  1. You can delete from the end of the Array, which might be constant time. O(1)
  2. However, you can also remove it from the beginning or middle of the collection. In that case, you would have to move all the following elements to close the gap. O(n)

Talk is cheap. Let’s do the code!

1
2
3
4
5
6
7
8
function remove(array, element) {
  const index = search(array, element);
  array.splice(index, 1);
  return array;
}

const array1 = [0, 1, 2, 3];
console.log(remove(array1, 1)); // => [ 0, 2, 3 ]

So we are using our search function to find the elements’ index O(n). Then we use the JS built-in splice function, which has a running time of O(n). What’s the total O(2n)? Remember, we constants don’t matter as much.

We take the worst-case scenario:

Deleting an item from an array is O(n).

Array operations time complexity

We can sum up the arrays time complexity as follows:

Array Time Complexities

Operation Worst
Access (Array.[]) O(1)
Insert head (Array.unshift) O(n)
Insert tail (Array.push) O(1)
Search (for value) O(n)
Delete (Array.splice) O(n)

HashMaps

Maps, dictionaries, and associative arrays all describe the same abstract data type. But hash map implementations are distinct from treemap implementations in that one uses a hash table and one uses a binary search tree.

Hashtable is a data structure that maps keys to values

Going back to the drawer analogy, bins have a label rather than a number.

HashMap is like a drawer that stores things on bins and labels them

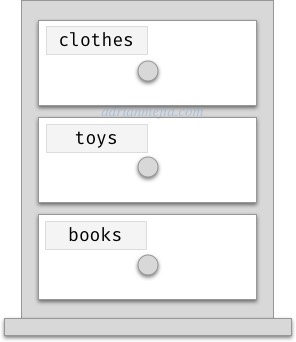
In this example, if you are looking for the book, you don’t have to open bin 1, 2, and 3. You go directly to the container labeled as “books”. That’s a huge gain! Search time goes from O(n) to O(1).

In arrays, the data is referenced using a numeric index (relatively to the position). However, HashMaps uses labels that could be a string, number, Object, or anything. Internally, the HashMap uses an Array, and it maps the labels to array indexes using a hash function.

There are at least two ways to implement hashmap:

  1. Array: Using a hash function to map a key to the array index value. Worst: O(n), Average: O(1)
  2. Binary Search Tree: using a self-balancing binary search tree to look up for values (more on this later). Worst: O(log n), Average: O(log n).

We will cover Trees & Binary Search Trees, so don’t worry about it for now. The most common implementation of Maps is using an array and hash function. So, that’s the one we are going to focus on.

HashMap implemented with an array

As you can see in the image, each key gets translated into a hash code. Since the array size is limited (e.g., 10), we have to loop through the available buckets using the modulus function. In the buckets, we store the key/value pair, and if there’s more than one, we use a collection to hold them.

Now, What do you think about covering each of the HashMap components in detail? Let’s start with the hash function.

HashMap vs. Array

Why go through the trouble of converting the key into an index and not using an array directly, you might ask. The main difference is that Array’s index doesn’t have any relationship with the data. You have to know where your data is.

Let’s say you want to count how many times words are used in a text. How would you implement that?

  1. You can use two arrays (let’s call it A and B). One for storing the word and another for storing how many times they have seen (frequency).
  2. You can use a HashMap. They key is the word, and the value is the word’s frequency.

What is the runtime of approach #1 using two arrays? If we say, the number of words in the text is n. Then we have to search if the word in the array A and then increment the value on array B matching that index. For every word on n, we have to test if it’s already on array A. This double loop leave use with a runtime of O(n2).

What is the runtime of approach #2 using a HashMap? We iterate through each word on the text once and increment the value if there is something there or set it to 1 if that word is seen for the first time. The runtime would be O(n), which is much more performant than approach #1.

Differences between HashMap and Array

  • Search on an array is O(n) while on a HashMap is O(1)
  • Arrays can have duplicate values, while HashMap cannot have duplicated keys (but they can have identical values.)
  • The Array has a key (index) that is always a number from 0 to max value, while in a HashMap, you have control of the key, and it can be whatever you want: number, string, or symbol.

Hash Function

The first step to implement a HashMap is to have a hash function. This function will map every key to its value.

The perfect hash function is the one that for every key, it assigns a unique index.

Ideal hashing algorithms allow constant time access/lookup. However, it’s hard to achieve a perfect hashing function in practice. You might have the case where two different keys yields on the same index, causing a collision.

Collisions in HashMaps are unavoidable when using an array-like underlying data structure. At some point, data that can’t fit in a HashMap will reuse data slots. One way to deal with collisions is to store multiple values in the same bucket using a linked list or another array (more on this later). When we try to access the key’s value and found various values, we iterate over the values O(n). However, in most implementations, the hash adjusts the size dynamically to avoid too many collisions. We can say that the amortized lookup time is O(1). We are going to explain what we mean by amortized runtime later in this post with an example.

Naïve HashMap implementation

A simple (and bad) hash function would be this one:

Naive HashMap Implementationfull code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class NaiveHashMap {

  constructor(initialCapacity = 2) {
    this.buckets = new Array(initialCapacity);
  }

  set(key, value) {
    const index = this.getIndex(key);
    this.buckets[index] = value;
  }

  get(key) {
    const index = this.getIndex(key);
    return this.buckets[index];
  }

  hash(key) {
    return key.toString().length;
  }

  getIndex(key) {
    const indexHash = this.hash(key);
    const index = indexHash % this.buckets.length;
    return index;
  }
}

We are using buckets rather than drawer/bins, but you get the idea :)

We have an initial capacity of 2 (two buckets). But, we want to store any number of elements on them. We use modulus % to loop through the number of available buckets.

Take a look at our hash function in line 18. We are going to talk about it in a bit. First, let’s use our new HashMap!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// Usage:
const assert = require('assert');
const hashMap = new NaiveHashMap();

hashMap.set('cat', 2);
hashMap.set('rat', 7);
hashMap.set('dog', 1);
hashMap.set('art', 8);

console.log(hashMap.buckets);
/*
  bucket #0: <1 empty item>,
  bucket #1: 8
*/

assert.equal(hashMap.get('art'), 8); // this one is ok
assert.equal(hashMap.get('cat'), 8); // got overwritten by art 😱
assert.equal(hashMap.get('rat'), 8); // got overwritten by art 😱
assert.equal(hashMap.get('dog'), 8); // got overwritten by art 😱

This Map allows us to set a key and a value and then get the value using a key. The key part is the hash function. Let’s see multiple implementations to see how it affects the Map’s performance.

Can you tell what’s wrong with NaiveHashMap before expanding the answer below?

What is wrong with `NaiveHashMap` is that...



1) Hash function generates many duplicates. E.g.

1
2
hash('cat') // 3
hash('dog') // 3

This hash implementation will cause a lot of collisions.



2) Collisions are not handled at all. Both cat and dog will overwrite each other on position 3 of the Array (bucket#1).



3) Size of the Array even if we get a better hash function, we will get duplicates because the Array has a size of 3, which less than the number of elements that we want to fit. We want to have an initial capacity that is well beyond what we need to fit.

Did you guess any? ☝️

Improving Hash Function

The primary purpose of a HashMap is to reduce the search/access time of an Array from O(n) to O(1).

For that, we need:

  1. A proper hash function that produces as few collisions as possible.
  2. An array big enough to hold all the required values.

Let’s give it another shot at our hash function. Instead of using the string’s length, let’s sum each character ascii code.

1
2
3
4
5
6
7
8
9
10
11
hash(key) {
  let hashValue = 0;
  const stringKey = key.toString();

  for (let index = 0; index < stringKey.length; index++) {
    const charCode = stringKey.charCodeAt(index);
    hashValue += charCode;
  }

  return hashValue;
}

Let’s try again:

1
2
hash('cat') // 312  (c=99 + a=97 + t=116)
hash('dog') // 314 (d=100 + o=111 + g=103)

This one is better! Because words with the same length have different codes.

Howeeeeeeeeever, there’s still an issue! Because rat and art are both 327, collision! 💥

We can fix that by offsetting the sum with the position:

1
2
3
4
5
6
7
8
9
10
11
hash(key) {
  let hashValue = 0;
  const stringKey = `${key}`;

  for (let index = 0; index < stringKey.length; index++) {
    const charCode = stringKey.charCodeAt(index);
    hashValue += charCode << (index * 8);
  }

  return hashValue;
}

Now let’s try again, this time with hex numbers so we can see the offset.

1
2
3
// r = 114 or 0x72; a = 97 or 0x61; t = 116 or 0x74
hash('rat'); // 7,627,122 (r: 114 * 1 + a: 97 * 256 + t: 116 * 65,536) or in hex: 0x746172 (r: 0x72 + a: 0x6100 + t: 0x740000)
hash('art'); // 7,631,457 or 0x747261

What about different types?

1
2
3
4
5
6
7
8
hash(1); // 49
hash('1'); // 49

hash('1,2,3'); // 741485668
hash([1,2,3]); // 741485668

hash('undefined') // 3402815551
hash(undefined) // 3402815551

Houston, we still have a problem!! Different value types shouldn’t return the same hash code!

How can we solve that?

One way is taking into account the key type into the hash function.

1
2
3
4
5
6
7
8
9
10
11
hash(key) {
  let hashValue = 0;
  const stringTypeKey = `${key}${typeof key}`;

  for (let index = 0; index < stringTypeKey.length; index++) {
    const charCode = stringTypeKey.charCodeAt(index);
    hashValue += charCode << (index * 8);
  }

  return hashValue;
}

Let’s test that again:

1
2
3
4
5
6
7
8
console.log(hash(1)); // 1843909523
console.log(hash('1')); // 1927012762

console.log(hash('1,2,3')); // 2668498381
console.log(hash([1,2,3])); // 2533949129

console.log(hash('undefined')); // 5329828264
console.log(hash(undefined)); // 6940203017

Yay!!! 🎉 We have a much better hash function!

We also can change the initial capacity of the Array to minimize collisions. Let’s put all of that together in the next section.

Decent HashMap Implementation

Using our optimized hash function, we can now do much better.

We could still have collisions, so let’s implement something to handle them.

Let’s make the following improvements to our HashMap implementation:

  • Hash function that checks types and character orders to minimize collisions.
  • Handle collisions by appending values to a list. We also added a counter to keep track of them.
Decent HashMap Implementationfull code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class DecentHashMap {

  constructor(initialCapacity = 2) {
    this.buckets = new Array(initialCapacity);
    this.collisions = 0;
  }

  set(key, value) {
    const bucketIndex = this.getIndex(key);
    if(this.buckets[bucketIndex]) {
      this.buckets[bucketIndex].push({key, value});
      if(this.buckets[bucketIndex].length > 1) { this.collisions++; }
    } else {
      this.buckets[bucketIndex] = [{key, value}];
    }
    return this;
  }

  get(key) {
    const bucketIndex = this.getIndex(key);
    for (let arrayIndex = 0; arrayIndex < this.buckets[bucketIndex].length; arrayIndex++) {
      const entry = this.buckets[bucketIndex][arrayIndex];
      if(entry.key === key) {
        return entry.value
      }
    }
  }

  hash(key) {
    let hashValue = 0;
    const stringTypeKey = `${key}${typeof key}`;

    for (let index = 0; index < stringTypeKey.length; index++) {
      const charCode = stringTypeKey.charCodeAt(index);
      hashValue += charCode << (index * 8);
    }

    return hashValue;
  }

  getIndex(key) {
    const indexHash = this.hash(key);
    const index = indexHash % this.buckets.length;
    return index;
  }
}

Let’s use it and see how it perform:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// Usage:
const assert = require('assert');
const hashMap = new DecentHashMap();

hashMap.set('cat', 2);
hashMap.set('rat', 7);
hashMap.set('dog', 1);
hashMap.set('art', 8);

console.log('collisions: ', hashMap.collisions); // 2
console.log(hashMap.buckets);
/*
  bucket #0: [ { key: 'cat', value: 2 }, { key: 'art', value: 8 } ]
  bucket #1: [ { key: 'rat', value: 7 }, { key: 'dog', value: 1 } ]
*/

assert.equal(hashMap.get('art'), 8); // this one is ok
assert.equal(hashMap.get('cat'), 2); // Good. Didn't got overwritten by art
assert.equal(hashMap.get('rat'), 7); // Good. Didn't got overwritten by art
assert.equal(hashMap.get('dog'), 1); // Good. Didn't got overwritten by art

This DecentHashMap gets the job done, but there are still some issues. We are using a decent hash function that doesn’t produce duplicate values, and that’s great. However, we have two values in bucket#0 and two more in bucket#1. How is that possible?

Since we are using a limited bucket size of 2, we use modulus % to loop through the number of available buckets. So, even if the hash code is different, all values will fit on the Array size: bucket#0 or bucket#1.

1
2
3
4
hash('cat') => 3789411390; bucketIndex => 3789411390 % 2 = 0
hash('art') => 3789415740; bucketIndex => 3789415740 % 2 = 0
hash('dog') => 3788563007; bucketIndex => 3788563007 % 2 = 1
hash('rat') => 3789411405; bucketIndex => 3789411405 % 2 = 1

So naturally, we have increased the initial capacity, but by how much? Let’s see how the initial size affects the hash map performance.

If we have an initial capacity of 1. All the values will go into one bucket (bucket#0), and it won’t be any better than searching a deal in a simple array O(n).

Let’s say that we start with an initial capacity set to 10:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const hashMapSize10 = new DecentHashMap(10);

hashMapSize10.set('cat', 2);
hashMapSize10.set('rat', 7);
hashMapSize10.set('dog', 1);
hashMapSize10.set('art', 8);

console.log('collisions: ', hashMapSize10.collisions); // 1
console.log('hashMapSize10\n', hashMapSize10.buckets);
/*
  bucket#0: [ { key: 'cat', value: 2 }, { key: 'art', value: 8 } ],
            <4 empty items>,
  bucket#5: [ { key: 'rat', value: 7 } ],
            <1 empty item>,
  bucket#7: [ { key: 'dog', value: 1 } ],
            <2 empty items>
*/

Another way to see this

As you can see, we reduced the number of collisions (from 2 to 1) by increasing the hash map’s initial capacity.

Let’s try with a bigger capacity 💯:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
const hashMapSize100 = new DecentHashMap(100);

hashMapSize100.set('cat', 2);
hashMapSize100.set('rat', 7);
hashMapSize100.set('dog', 1);
hashMapSize100.set('art', 8);

console.log('collisions: ', hashMapSize100.collisions); // 0
console.log('hashMapSize100\n', hashMapSize100.buckets);
/*
            <5 empty items>,
  bucket#5: [ { key: 'rat', value: 7 } ],
            <1 empty item>,
  bucket#7: [ { key: 'dog', value: 1 } ],
            <32 empty items>,
  bucket#41: [ { key: 'art', value: 8 } ],
            <49 empty items>,
  bucket#90: [ { key: 'cat', value: 2 } ],
            <9 empty items>
*/

Yay! 🎊 no collision!

Having a bigger bucket size is excellent to avoid collisions, but it consumes too much memory, and probably most of the buckets will be unused.

Wouldn’t it be great if we can have a HashMap that automatically increases its size as needed? Well, that’s called ** rehash**, and we are going to do it next!

Optimal HashMap Implementation

If we have a big enough bucket, we won’t have collisions; thus, the search time would be O(1). However, how do we know how big a hash map capacity should big? 100? 1,000? A million?

Having allocated massive amounts of memory is impractical. So, we can automatically have the hash map resize itself based on a load factor. This operation is called ** rehash**.

The load factor is the measurement of how full is a hash map. We can get the load factor by dividing the number of items by the bucket size.

This will be our latest and greatest hash map implementation:

**Optimized Hash Map Implementation _(click here to show the code)_**
Optimal HashMap Implementationdocumented code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115

class HashMap {
  constructor(initialCapacity = 16, loadFactor = 0.75) {
    this.buckets = new Array(initialCapacity);
    this.loadFactor = loadFactor;
    this.size = 0;
    this.collisions = 0;
    this.keys = [];
  }

  hash(key) {
    let hashValue = 0;
    const stringTypeKey = `${key}${typeof key}`;

    for (let index = 0; index < stringTypeKey.length; index++) {
      const charCode = stringTypeKey.charCodeAt(index);
      hashValue += charCode << (index * 8);
    }

    return hashValue;
  }


  _getBucketIndex(key) {
    const hashValue = this.hash(key);
    const bucketIndex = hashValue % this.buckets.length;
    return bucketIndex;
  }

  set(key, value) {
    const {bucketIndex, entryIndex} = this._getIndexes(key);

    if(entryIndex === undefined) {
      // initialize array and save key/value
      const keyIndex = this.keys.push({content: key}) - 1; // keep track of the key index
      this.buckets[bucketIndex] = this.buckets[bucketIndex] || [];
      this.buckets[bucketIndex].push({key, value, keyIndex});
      this.size++;
      // Optional: keep count of collisions
      if(this.buckets[bucketIndex].length > 1) { this.collisions++; }
    } else {
      // override existing value
      this.buckets[bucketIndex][entryIndex].value = value;
    }

    // check if a rehash is due
    if(this.loadFactor > 0 && this.getLoadFactor() > this.loadFactor) {
      this.rehash(this.buckets.length * 2);
    }

    return this;
  }

  get(key) {
    const {bucketIndex, entryIndex} = this._getIndexes(key);

    if(entryIndex === undefined) {
      return;
    }

    return this.buckets[bucketIndex][entryIndex].value;
  }

  has(key) {
    return !!this.get(key);
  }

  _getIndexes(key) {
    const bucketIndex = this._getBucketIndex(key);
    const values = this.buckets[bucketIndex] || [];

    for (let entryIndex = 0; entryIndex < values.length; entryIndex++) {
      const entry = values[entryIndex];
      if(entry.key === key) {
        return {bucketIndex, entryIndex};
      }
    }

    return {bucketIndex};
  }

  delete(key) {
    const {bucketIndex, entryIndex, keyIndex} = this._getIndexes(key);

    if(entryIndex === undefined) {
      return false;
    }

    this.buckets[bucketIndex].splice(entryIndex, 1);
    delete this.keys[keyIndex];
    this.size--;

    return true;
  }

  rehash(newCapacity) {
    const newMap = new HashMap(newCapacity);

    this.keys.forEach(key => {
      if(key) {
        newMap.set(key.content, this.get(key.content));
      }
    });

    // update bucket
    this.buckets = newMap.buckets;
    this.collisions = newMap.collisions;
    // Optional: both `keys` has the same content except that the new one doesn't have empty spaces from deletions
    this.keys = newMap.keys;
  }

  getLoadFactor() {
    return this.size / this.buckets.length;
  }
}

Pay special attention to lines 96 to 114. That’s where the rehash magic happens. We create a new HashMap with doubled capacity.

So, testing our new implementation from above ^

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
const assert = require('assert');
const hashMap = new HashMap();

assert.equal(hashMap.getLoadFactor(), 0);
hashMap.set('songs', 2);
hashMap.set('pets', 7);
hashMap.set('tests', 1);
hashMap.set('art', 8);
assert.equal(hashMap.getLoadFactor(), 4/16);

hashMap.set('Pineapple', 'Pen Pineapple Apple Pen');
hashMap.set('Despacito', 'Luis Fonsi');
hashMap.set('Bailando', 'Enrique Iglesias');
hashMap.set('Dura', 'Daddy Yankee');

hashMap.set('Lean On', 'Major Lazer');
hashMap.set('Hello', 'Adele');
hashMap.set('All About That Bass', 'Meghan Trainor');
hashMap.set('This Is What You Came For', 'Calvin Harris ');

assert.equal(hashMap.collisions, 2);
assert.equal(hashMap.getLoadFactor(), 0.75);
assert.equal(hashMap.buckets.length, 16);

hashMap.set('Wake Me Up', 'Avicii'); // <--- Trigger REHASH

assert.equal(hashMap.collisions, 0);
assert.equal(hashMap.getLoadFactor(), 0.40625);
assert.equal(hashMap.buckets.length, 32);

Take notice that after we add the 12th item, the load factor gets beyond 0.75, so a rehash is triggered and doubles the capacity (from 16 to 32). Also, you can see how the number of collisions improves from 2 to 0!

This implementation is good enough to help us figure out the runtime of standard operations like insert/search/delete/edit.

To sum up, the performance of a HashMap will be given by:

  1. The hash function that every key produces for different output.
  2. Size of the bucket to hold data.

We nailed both 🔨. We have a decent hash function that produces different outputs for different data. Two distinct data will never return the same code. Also, we have a rehash function that automatically grows the capacity as needed. That’s great!

Insert element on a HashMap runtime

Inserting an element on a HashMap requires two things: a key and a value. We could use our DecentHashMap data structure that we develop or use the built-in as follows:

1
2
3
4
5
6
7
function insert(object, key, value) {
  object[key] = value;
  return object;
}

const object = {};
console.log(insert(hash, 'word', 1)); // => { word: 1 }

In modern JavaScript, you can use Maps.

1
2
3
4
5
6
7
function insertMap(map, key, value) {
  map.set(key, value);
  return map;
}

const map = new Map();
console.log(insertMap(map, 'word', 1)); // Map { 'word' => 1 }

Note: We will use the Map rather than the regular Object, since the Map’s key could be anything while on Object’s key can only be string or number. Also, Maps keeps the order of insertion.

Behind the scenes, the Map.set just insert elements into an array (take a look at DecentHashMap.set). So, similar to Array.push we have that:

Insert an element in HashMap runtime is O(1). If rehash is needed, then it will take O(n)

Our implementation with rehash functionality will keep collisions to the minimum. The rehash operation takes O(n), but it doesn’t happen all the time, only when it is needed.

Search/Access an element on a HashMap runtime

This is the HashMap.get function that we use to get the value associated with a key. Let’s evaluate the implementation from DecentHashMap.get):

1
2
3
4
5
6
7
8
9
10
get(key) {
  const hashIndex = this.getIndex(key);
  const values = this.array[hashIndex];
  for (let index = 0; index < values.length; index++) {
    const entry = values[index];
    if(entry.key === key) {
      return entry.value
    }
  }
}

If there’s no collision, then values will only have one value, and the access time would be O(1). But, we know there will be collisions. If the initial capacity is too small and the hash function is terrible like NaiveHashMap.hash, then most of the elements will end up in a few buckets O(n).

HashMap access operation has a runtime of O(1) on average and worst-case of O(n).

Advanced Note: Another idea to reduce the time to get elements from O(n) to O(log n) is to use a binary search tree instead of an array. Actually, Java’s HashMap implementation switches from an array to a tree when a bucket has more than 8 elements.

Edit/Delete element on a HashMap runtime

Editing (HashMap.set) and deleting (HashMap.delete) key/value pairs have an amortized runtime of O(1). In the case of many collisions, we could face an O(n) as a worst-case. However, with our rehash operation, we can mitigate that risk.

HashMap edits and delete operations has a runtime of O(1) on average and worst-case of O(n).

HashMap operations time complexity

We can sum up the arrays time complexity as follows:

HashMap Time Complexities

Operation Worst Amortized Comments
Access/Search (HashMap.get) O(n) O(1) O(n) is an extreme case when there are too many collisions
Insert/Edit (HashMap.set) O(n) O(1) O(n) only happens with rehash when the Hash is 0.75 full
Delete (HashMap.delete) O(n) O(1) O(n) is an extreme case when there are too many collisions

Sets

Sets are very similar to arrays. The difference is that they don’t allow duplicates.

How can we implement a Set (Array without duplicates)? We could use an array and check if an element is there before inserting a new one. But the running time of checking if a value is already there is O(n). Can we do better than that? We develop the Map with an amortized run time of O(1)!

Set Implementation

We could use the JavaScript built-in Set. However, if we implement it by ourselves, it’s more logical to deduct the runtimes. We are going to use the optimized HashMap with rehash functionality.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
const HashMap = require('../hash-maps/hash-map');

class MySet {
  constructor() {
    this.hashMap = new HashMap();
  }

  add(value) {
    this.hashMap.set(value);
  }

  has(value) {
    return this.hashMap.has(value);
  }

  get size() {
    return this.hashMap.size;
  }

  delete(value) {
    return this.hashMap.delete(value);
  }

  entries() {
    return this.hashMap.keys.reduce((acc, key) => {
      if(key !== undefined) {
        acc.push(key.content);
      }
      return acc
    }, []);
  }
}

We used HashMap.set to add the set elements without duplicates. We use the key as the value, and since the hash map’s keys are unique, we are all set.

Checking if an element is already there can be done using the hashMap.has, which has an amortized runtime of O(1). Most operations would be an amortized constant time except for getting the entries, O(n).

Note: The JS built-in Set.has has a runtime of O(n) since it uses a regular list of elements and checks each one at a time. You can see the Set.has algorithm here

Here some examples how to use it:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
const assert = require('assert');
// const set = new Set(); // Using the built-in
const set = new MySet(); // Using our own implementation

set.add('one');
set.add('uno');
set.add('one'); // should NOT add this one twice

assert.equal(set.has('one'), true);
assert.equal(set.has('dos'), false);

assert.equal(set.size, 2);
// assert.deepEqual(Array.from(set), ['one', 'uno']);

assert.equal(set.delete('one'), true);
assert.equal(set.delete('one'), false);
assert.equal(set.has('one'), false);
assert.equal(set.size, 1);

You should be able to use MySet and the built-in Set interchangeably for these examples.

Set Operations runtime

From our Set implementation using a HashMap, we can sum up the time complexity as follows (very similar to the HashMap):

Set Time Complexities

Operation Worst Amortized Comments
Access/Search (Set.has) O(n) O(1) O(n) is an extreme case when there are too many collisions
Insert/Edit (Set.add) O(n) O(1) O(n) only happens with rehash when the Hash is 0.75 full
Delete (Set.delete) O(n) O(1) O(n) is an extreme case when there are too many collisions

Linked Lists

A linked list is a data structure where every element is connected to the next one.

The linked list is the first data structure that we are going to implement without using an array. Instead, we will use a node that holds a value and points to the next element.

node.js
1
2
3
4
5
6
class Node {
  constructor(value) {
    this.value = value;
    this.next = null;
  }
}

When we have a chain of nodes where each one points to the next one, we a Singly Linked list.

Singly Linked Lists

For a singly linked list, we only have to worry about every element referencing the next one.

We start by constructing the root or head element.

linked-list.js
1
2
3
4
5
6
7
8
class LinkedList {
  constructor() {
    this.root = null; // first/head/root element
    this.size = 0; // total number of elements in the list
  }

  // ...
}

There are four basic operations that we can do in every Linked List:

  1. addLast: appends an element to the end of the list (tail)
  2. removeLast: deletes element to the end of the list
  3. addFirst: Adds an element to the beginning of the list (head)
  4. removeFirst: Removes an element from the start of the list (head/root)

Adding/Removing an element at the end of a linked list

There are two primary cases:

  1. If the list first (root/head) doesn’t have any element yet, we make this node the head of the list.
  2. Contrary, if the list already has items, then we have to iterate until finding the last one and appending our new node to the end.

LinkedList.prototype.addLast
1
2
3
4
5
6
7
8
9
10
11
12
13
addLast(value) { // similar Array.push
  const node = new Node(value);

  if(this.root) {
    let currentNode = this.root;
    while(currentNode && currentNode.next) {
      currentNode = currentNode.next;
    }
    currentNode.next = node;
  } else {
    this.root = node;
  }
}

What’s the runtime of this code? If it is the first element, then adding to the root is O(1). However, finding the last item is O(n).

Now, removing an element from the end of the list has a similar code. We have to find the current before last and make its next reference null.

LinkedList.prototype.removeLast
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
removeLast() {
  let current = this.root;
  let target;

  if(current && current.next) {
    while(current && current.next && current.next.next) {
      current = current.next;
    }
    target = current.next;
    current.next = null;
  } else {
    this.root = null;
    target = current;
  }

  if(target) {
    return target.value;
  }
}

The runtime again is O(n) because we have to iterate until the second-last element and remove the reference to the last (line 10).

Adding/Removing an element from the beginning of a linked list

Adding an element to the head of the list is like this:

LinkedList.addFirst
1
2
3
4
5
6
7
8
9
10
/**
  * Adds an element to the beginning of the list. Similar to Array.unshift
  * Runtime: O(1)
  * @param {any} value
  */
addFirst(value) {
  const node = new Node(value);
  node.next = this.root;
  this.root = node;
}

Adding and removing elements from the beginning is a constant time because we hold a reference to the first element:

LinkedList.removeFirst
1
2
3
4
5
6
7
8
9
10
11
12
/**
  * Removes element from the start of the list (head/root). It's Similar `Array.shift`
  * Runtime: O(1)
  */
removeFirst() {
  const first = this.root;

  if (first) {
    this.root = first.next;
    return first.value;
  }
}

As expected, the runtime for removing/adding to the first element from a linked List is always constant O(1)

Removing an element anywhere from a linked list

Removing an element anywhere in the list leverage the removeLast and removeFirst. However, if the removal is in the middle, then we assign the previous node to the next one. That removes any reference from the current node, this is removed from the list:

LinkedList.remove
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
remove(index = 0) {
  if(index === 0) {
    return this.removeFirst();
  }

  for (let current = this.first, i = 0; current;  i++, current = current.next) {
    if(i === index) {
      if(!current.next) { // if it doesn't have next it means that it is the last
        return this.removeLast();
      }
      current.previous.next = current.next;
      this.size--;
      return current.value;
    }
  }
}

Note that index is a zero-based index: 0 will be the first element, 1 second, and so on.

Removing an element anywhere within the list is O(n).

Searching for an element in a linked list

Searching an element on the linked list is very somewhat similar to remove:

LinkedList.contains
1
2
3
4
5
6
7
contains(value) {
  for (let current = this.first, index = 0; current;  index++, current = current.next) {
    if(current.value === value) {
      return index;
    }
  }
}

This function finds the first element with the given value.

The runtime for searching an element in a linked list is O(n)

Singly Linked Lists time complexity

Singly Linked List time complexity per function is as follows.

Operation Runtime Comment
addFirst O(1) Insert element to the beginning of the list
addLast O(n) Insert element to the end of the list
add O(n) Insert element anywhere in the list.
removeFirst O(1) Remove element to the beginning of the list
removeLast O(n) Remove element to the end of the list
remove O(n) Remove any element from the list
contains O(n) Search for an element from the list

Notice that every time we add/remove from the last position, the operation takes O(n).

But we could reduce the addLast/removeLast from O(n) to a flat O(1) if we keep a reference of the last element!

We are going to add the last reference in the next section!

Doubly Linked Lists

When we have a chain of nodes where each one points to the next one, we have a Singly Linked list. When we have a linked list where each node leads to the next and the previous element, we have a Doubly Linked List

Doubly linked list nodes have double references (next and previous). We are also going to keep track of the list first and the last element.

Doubly Linked Listfull code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Node {
  constructor(value) {
    this.value = value;
    this.next = null;
    this.previous = null;
  }
}

class LinkedList {
  constructor() {
    this.first = null; // head/root element
    this.last = null; // last element of the list
    this.size = 0; // total number of elements in the list
  }

  // ...
}

Adding and Removing from the start of a list

Adding and removing from the start of the list is simple since we have this.first reference:

LinkedList.prototype.addFirstfull code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
addFirst(value) {
  const node = new Node(value);

  node.next = this.first;

  if(this.first) {
    this.first.previous = node;
  } else {
    this.last = node;
  }

  this.first = node; // update head
  this.size++;

  return node;
}

Notice that we have to be very careful and update the previous and last reference.

LinkedList.prototype.removeFirstfull code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
removeFirst() {
  const first = this.first;

  if(first) {
    this.first = first.next;
    if(this.first) {
      this.first.previous = null;
    }

    this.size--;

    return first.value;
  } else {
    this.last = null;
  }
}

What’s the runtime?

Adding and removing elements from a (singly/doubly) LinkedList has a constant runtime O(1)

Adding and removing from the end of a list

Adding and removing from the end of the list is a little tricky. If you checked in the Singly Linked List, both operations took O(n) since we had to loop through the list to find the last element. Now, we have the last reference:

LinkedList.prototype.addLastfull code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
addLast(value) {
  const node = new Node(value);

  if(this.first) {
    let currentNode = this.first;
    node.previous = this.last;
    this.last.next = node;
    this.last = node;
  } else {
    this.first = node;
    this.last = node;
  }

  this.size++;

  return node;
}

Again, we have to be careful about updating the references and handling exceptional cases such as only one element.

LinkedList.prototype.removeLastfull code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
removeLast() {
  let current = this.first;
  let target;

  if(current && current.next) {
    current = this.last.previous;
    this.last = current;
    target = current.next;
    current.next = null;
  } else {
    this.first = null;
    this.last = null;
    target = current;
  }

  if(target) {
    this.size--;
    return target.value;
  }
}

Using a doubly-linked list, we no longer have to iterate through the whole list to get the 2nd last element. We can use directly this.last.previous and is O(1).

Did you remember that for the Queue, we had to use two arrays? We can now change that implementation and use a doubly-linked list instead. The runtime will be O(1) for insert at the start and deleting at the end.

Adding an element anywhere from a linked list

Adding an element on anywhere on the list leverages our addFirst and addLast functions as you can see below:

LinkedList.addFullCode
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
add(value, index = 0) {
  if(index === 0) {
    return this.addFirst(value);
  }

  for (let current = this.first, i = 0; i <= this.size;  i++, current = (current && current.next)) {
    if(i === index) {
      if(i === this.size) { // if it doesn't have next it means that it is the last
        return this.addLast(value);
      }
      const newNode = new Node(value);
      newNode.previous = current.previous;
      newNode.next = current;

      current.previous.next = newNode;
      if(current.next) { current.next.previous = newNode; }
      this.size++;
      return newNode;
    }
  }
}

If we have an insertion in the middle of the Array, then we have to update the next and previous reference of the surrounding elements.

Adding an element anywhere within the list is O(n).

Doubly Linked Lists time complexity

Doubly Linked List time complexity per function is as follows:

Operation Runtime Comment
addFirst O(1) Insert element to the beginning of the list.
addLast O(1) Insert element to the end of the list.
add O(n) Insert element anywhere in the list.
removeFirst O(1) Remove element to the beginning of the list.
removeLast O(1) Remove element to the end of the list.
remove O(n) Remove any element from the list
contains O(n) Search for any element from the list

Doubly linked lists are a significant improvement compared to the singly linked list! We improved from O(n) to O(1) by:

  • Adding a reference to the previous element.
  • Holding a reference to the last item in the list.

Removing first/last can be done in constant time; however, eliminating in the middle of the Array is still O(n).

Stacks

Stacks is a data structure where the last entered data is the first to come out. Also know as Last-in, First-out (LIFO).

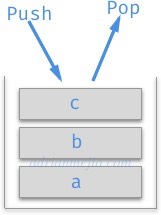
Let’s implement a stack from scratch!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Stack {
  constructor() {
    this.input = [];
  }

  push(element) {
    this.input.push(element);
    return this;
  }

  pop() {
    return this.input.pop();
  }
}

As you can see, it is easy since we are using the built-in Array.push and Array.pop. Both have a runtime of O(1).

Let’s see some examples of its usage:

1
2
3
4
5
6
7
8
9
const stack = new Stack();

stack.push('a');
stack.push('b');
stack.push('c');

stack.pop(); // c
stack.pop(); // b
stack.pop(); // a

The first element in (a) is the last to get out. We can also implement Stack using a linked list instead of an array. The runtime will be the same.

That’s all!

Queues

Queues are a data structure where the first data to get in is also the first to go out. A.k.a First-in, First-out (FIFO). It’s like a line of people at the movies, the first to come in is the first to come out.

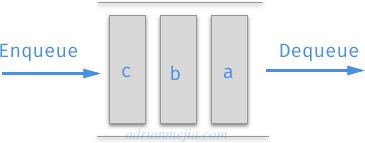
We could implement a Queue using an array, very similar to how we implemented the Stack.

Queue implemented with Array(s)

A naive implementation would be this one using Array.push and Array.shift:

1
2
3
4
5
6
7
8
9
10
11
12
13
class Queue {
  constructor() {
    this.input = [];
  }

  add(element) {
    this.input.push(element);
  }

  remove() {
    return this.input.shift();
  }
}

What’s the time complexity of Queue.add and Queue.remove?

  • Queue.add uses array.push which has a constant runtime. Win!
  • Queue.remove uses array.shift which has a linear runtime. Can we do better than O(n)?

Think of how you can implement a Queue only using Array.push and Array.pop.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Queue {
  constructor() {
    this.input = [];
    this.output = [];
  }

  add(element) {
    this.input.push(element);
  }

  remove() {
    if(!this.output.length) {
      while(this.input.length) {
        this.output.push(this.input.pop());
      }
    }
    return this.output.pop();
  }
}

Now we are using two arrays rather than one.

1
2
3
4
5
6
7
8
9
const queue = new Queue();

queue.add('a');
queue.add('b');

queue.remove() // a
queue.add('c');
queue.remove() // b
queue.remove() // c

When we remove something for the first time, the output array is empty. So, we insert the content of input backward like ['b', 'a']. Then we pop elements from the output array. As you can see, using this trick, we get the output in the same order of insertion (FIFO).

What’s the runtime?

If the output already has some elements, then the remove operation is constant O(1). When the output arrays need to get refilled, it takes O(n) to do so. After the refilled, every operation would be constant again. The amortized time is O(1).

We can achieve a Queue with a pure constant if we use LinkedList. Let’s see what it is in the next section!

Queue implemented with a Doubly Linked List

We can achieve the best performance for a queue using a linked list rather than an array.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const LinkedList = require('../linked-lists/linked-list');

class Queue {
  constructor() {
    this.input = new LinkedList();
  }

  add(element) {
    this.input.addFirst(element);
  }

  remove() {
    return this.input.removeLast();
  }

  get size() {
    return this.input.size;
  }
}

Using a doubly-linked list with the last element reference, we achieve an add of O(1). That’s the importance of using the right tool for the right job. 💪

Summary

We explored most of the linear data structures. We saw that depending on how we implement the data structures. There are different runtimes.

Here’s a summary of everything that we explored. You can click on each runtime, and it will take you to the implementation.

Time complexity

Click on the name to go to the section or click on the runtime to go to the implementation

* = Amortized runtime

Name Insert Access Search Delete Comments
Array O(n) O(1) O(n) O(n) Insertion to the end is O(1). Details here.
HashMap O(1) O(1) O(1) O(1) Rehashing might affect insertion time. Details here.
Map (using Binary Search Tree) O(log(n)) - O(log(n)) O(log(n)) Implemented using Binary Search Tree
Set (using HashMap) O(1) - O(1) O(1) Set using a HashMap implementation. Details here.
Set (using list) O(n) - O(n) O(n) Implemented using Binary Search Tree
Set (using Binary Search Tree) O(log(n)) - O(log(n)) O(log(n)) Implemented using Binary Search Tree
Linked List (singly) O(n) - O(n) O(n) Adding/Removing to the start of the list is O(1). Details here.
Linked List (doubly) O(n) - O(n) O(n) Adding/Deleting from the beginning/end is O(1). But, deleting/adding from the middle is O(n). Details here
Stack (array implementation) O(1) - - O(1) Insert/delete is last-in, first-out (LIFO)
Queue (naïve array impl.) O(1) - - O(n) Remove (Array.shift) is O(n)
Queue (array implementation) O(1) - - O(1) Worst time insert is O(n). However amortized is O(1)
Queue (list implementation) O(1) - - O(1) Using Doubly Linked List with reference to the last element.

Note: Binary search trees and trees, in general, will be cover in the next post. Also, graph data structures.